
Model-based mediation and moderation analyses (named after but distinct from SPSS PROCESS).
Source:R/bruceR-stats_5_advance.R
PROCESS.RdModel-based mediation and moderation analyses (i.e., using raw regression model objects with distinct R packages, BUT NOT with the SPSS PROCESS Macro, to estimate effects in mediation/moderation models).
NOTE: PROCESS() DOES NOT use or transform any code or macro from the original SPSS PROCESS macro developed by Hayes, though its output would link model settings to a PROCESS Model ID in Hayes's numbering system.
To use PROCESS() in publications, please cite not only bruceR but also the following R packages:
interactions::sim_slopes()is used to estimate simple slopes (and conditional direct effects) in moderation, moderated moderation, and moderated mediation models (for PROCESS Model IDs 1, 2, 3, 5, 7, 8, 9, 10, 11, 12, 14, 15, 16, 17, 18, 19, 58, 59, 72, 73, 75, 76).mediation::mediate()is used to estimate (conditional) indirect effects in (moderated) mediation models (for PROCESS Model IDs 4, 5, 7, 8, 9, 10, 11, 12, 14, 15, 16, 17, 18, 19, 58, 59, 72, 73, 75, 76).lavaan::sem()is used to perform serial multiple mediation analysis (for PROCESS Model ID 6).
Usage
PROCESS(
data,
y = "",
x = "",
meds = c(),
mods = c(),
covs = c(),
clusters = c(),
hlm.re.m = "",
hlm.re.y = "",
hlm.type = c("1-1-1", "2-1-1", "2-2-1"),
med.type = c("parallel", "serial"),
mod.type = c("2-way", "3-way"),
mod.path = c("x-y", "x-m", "m-y", "all"),
cov.path = c("y", "m", "both"),
mod1.val = NULL,
mod2.val = NULL,
ci = c("boot", "bc.boot", "bca.boot", "mcmc"),
nsim = 100,
seed = NULL,
center = TRUE,
std = FALSE,
digits = 3,
file = NULL
)Arguments
- data
Data frame.
- y, x
Variable name of outcome (Y) and predictor (X).
Can be: continuous (numeric) or dichotomous (factor)
- meds
Variable name(s) of mediator(s) (M). Use
c()to combine multiple mediators.Can be: continuous (numeric) or dichotomous (factor)
Allows any number of mediators in parallel or 2~4 mediators in serial
Order matters when
med.type="serial"(PROCESS Model 6: serial mediation)
- mods
Variable name(s) of 0~2 moderator(s) (W). Use
c()to combine multiple moderators.Can be: continuous (numeric), dichotomous (factor), or multicategorical (factor)
Order matters when
mod.type="3-way"(PROCESS Models 3, 5.3, 11, 12, 18, 19, 72, and 73)Not applicable to
med.type="serial"(PROCESS Model 6)
- covs
Variable name(s) of covariate(s) (i.e., control variables). Use
c()to combine multiple covariates.Can be any type and any number of variables
- clusters
HLM (multilevel) cluster(s): e.g.,
"School",c("Prov", "City"),c("Sub", "Item").- hlm.re.m, hlm.re.y
HLM (multilevel) random effect term of M model and Y model. By default, it converts
clusterstolme4syntax of random intercepts: e.g.,"(1 | School)"or"(1 | Sub) + (1 | Item)".You may specify these arguments to include more complex terms: e.g., random slopes
"(X | School)", or 3-level random effects"(1 | Prov/City)".- hlm.type
HLM (multilevel) mediation type (levels of "X-M-Y"):
"1-1-1"(default),"2-1-1"(indeed the same as"1-1-1"in a mixed model), or"2-2-1"(currently not fully supported, as limited by themediationpackage). In most cases, no need to set this argument.- med.type
Type of mediator:
"parallel"(default) or"serial"(only relevant to PROCESS Model 6). Partial matches with"p"or"s"also work. In most cases, no need to set this argument.- mod.type
Type of moderator:
"2-way"(default) or"3-way"(relevant to PROCESS Models 3, 5.3, 11, 12, 18, 19, 72, and 73). Partial matches with"2"or"3"also work.- mod.path
Which path(s) do the moderator(s) influence?
"x-y","x-m","m-y", or any combination of them (usec()to combine), or"all"(i.e., all of them). No default value.- cov.path
Which path(s) do the control variable(s) influence?
"y","m", or"both"(default).- mod1.val, mod2.val
By default (
NULL), it uses Mean +/- SD of a continuous moderator (numeric) or all levels of a dichotomous/multicategorical moderator (factor) to perform simple slope analyses and/or conditional mediation analyses. You may manually specify a vector of certain values: e.g.,mod1.val=c(1, 3, 5)ormod1.val=c("A", "B", "C").- ci
Method for estimating the standard error (SE) and 95% confidence interval (CI) of indirect effect(s). Defaults to
"boot"for (generalized) linear models or"mcmc"for (generalized) linear mixed models (i.e., multilevel models)."boot": Percentile Bootstrap"bc.boot": Bias-Corrected Percentile Bootstrap"bca.boot": Bias-Corrected and Accelerated (BCa) Percentile Bootstrap"mcmc": Markov Chain Monte Carlo (Quasi-Bayesian)
Note that these methods never apply to the estimates of simple slopes. You should not report the 95% CIs of simple slopes as Bootstrap or Monte Carlo CIs, because they are just standard CIs without any resampling method.
- nsim
Number of simulation samples (bootstrap resampling or Monte Carlo simulation) for estimating SE and 95% CI. Defaults to
100for running examples faster. In formal analyses, however,nsim=1000(or larger) is strongly suggested!- seed
Random seed for reproducible results. Defaults to
NULL. Note that all mediation analyses include random processes (i.e., bootstrap resampling or Monte Carlo simulation). To reproduce results, you need to set a random seed. However, even if you set the same seed number, it is unlikely to get exactly the same results across different R packages (e.g.,lavaanvs.mediation) and software (e.g., SPSS, Mplus, R, jamovi).- center
Centering numeric (continuous) predictors? Defaults to
TRUE(suggested).- std
Standardizing variables to get standardized coefficients? Defaults to
FALSE. IfTRUE, it will standardize all numeric (continuous) variables before building regression models. However, it is not suggested to setstd=TRUEfor generalized linear (mixed) models.- digits
Number of decimal places of output. Defaults to
3.- file
File name of MS Word (
".doc"). Currently, only regression model summary can be saved.
Value
Invisibly return a list of results:
process.idPROCESS Model ID (in Hayes's numbering system).
process.typePROCESS model type.
model.mMediator (M) model(s) (a list of multiple models).
model.yOutcome (Y) model.
resultsEffect estimates and other results (unnamed list object).
Output
Two parts of results are printed:
PART 1. Regression model summary
PART 2. Mediation/moderation effect estimates
Disclaimer
PROCESS() DOES NOT use or transform any code or macro from the original SPSS PROCESS macro developed by Hayes, though its output would link model settings to a PROCESS Model ID in Hayes's numbering system.
DO NOT state that "the bruceR package runs the PROCESS Model Code developed by Hayes (2018)" — it was not the truth. The bruceR package only links results to Hayes's numbering system but never uses his code.
Software Comparison
To perform mediation, moderation, and conditional process (moderated mediation) analyses, people may use Mplus, SPSS "PROCESS" macro, or SPSS "MLmed" macro. Some R packages and functions can also perform such analyses, in a somewhat complex way, including mediation::mediate(), interactions::sim_slopes(), and lavaan::sem().
Furthermore, some other R packages or scripts/modules have been developed, including jamovi module jAMM (by Marcello Gallucci, based on the lavaan package), R package processR (by Keon-Woong Moon, not official, also based on the lavaan package), and R script file "process.R" (the official PROCESS R code by Andrew F. Hayes, but it is not yet an R package).
Distinct from these existing tools, PROCESS() provides an integrative way for performing mediation/moderation analyses in R. This function supports 24 kinds of SPSS PROCESS models numbered by Hayes (2018) (but does not use or transform his code), and also supports multilevel mediation/moderation analyses. Overall, it supports the most frequently used types of mediation, moderation, moderated moderation (3-way interaction), and moderated mediation (conditional indirect effect) analyses for (generalized) linear or linear mixed models.
Specifically, PROCESS() fits regression models based on the data, variable names, and a few other arguments that users input (with no need to specify the PROCESS Model ID or manually mean-center the variables). The function can automatically link model settings to Hayes's numbering system.
Variable Centering
PROCESS() automatically conducts grand-mean centering, using grand_mean_center(), before model building, though it can be turned off by setting center=FALSE.
The grand-mean centering is important because it:
makes the results of main effects accurate for interpretation (see my commentary on this issue: Bao et al., 2022);
does not change any model fit indices (it only affects the interpretation of main effects);
is only conducted in "PART 1" (for an accurate estimate of main effects) but not in "PART 2" because it is more intuitive and interpretable to use the raw values of variables for the simple-slope tests in "PART 2";
is not conflicted with group-mean centering because after group-mean centering the grand mean of a variable will also be 0, such that the automatic grand-mean centering (with mean = 0) will not change any values of the variable.
Conduct group-mean centering, if necessary, with group_mean_center() before using PROCESS(). Remember that the automatic grand-mean centering never affects the values of a group-mean centered variable, which already has a grand mean of 0.
References
Hayes, A. F. (2018). Introduction to mediation, moderation, and conditional process analysis (second edition): A regression-based approach. Guilford Press.
Yzerbyt, V., Muller, D., Batailler, C., & Judd, C. M. (2018). New recommendations for testing indirect effects in mediational models: The need to report and test component paths. Journal of Personality and Social Psychology, 115(6), 929–943.
See also
For more details and illustrations, see PROCESS-bruceR-SPSS (PDF and Markdown files).
Examples
#### NOTE ####
## In the following examples, I set nsim=100 to save time.
## In formal analyses, nsim=1000 (or larger) is suggested!
#### Demo Data ####
# ?mediation::student
data = mediation::student %>%
dplyr::select(SCH_ID, free, smorale, pared, income,
gender, work, attachment, fight, late, score)
names(data)[2:3] = c("SCH_free", "SCH_morale")
names(data)[4:7] = c("parent_edu", "family_inc", "gender", "partjob")
data$gender01 = 1 - data$gender # 0 = female, 1 = male
# dichotomous X: as.factor()
data$gender = factor(data$gender01, levels=0:1, labels=c("Female", "Male"))
# dichotomous Y: as.factor()
data$pass = as.factor(ifelse(data$score>=50, 1, 0))
#### Descriptive Statistics and Correlation Analyses ####
Freq(data$gender)
#> Frequency Statistics:
#> ─────────────────
#> N %
#> ─────────────────
#> Female 5044 52.1
#> Male 4635 47.9
#> ─────────────────
#> Total N = 9,679
Freq(data$pass)
#> Frequency Statistics:
#> ────────────
#> N %
#> ────────────
#> 0 3856 39.8
#> 1 5823 60.2
#> ────────────
#> Total N = 9,679
Describe(data) # file="xxx.doc"
#> NOTE: `gender`, `pass` transformed to numeric.
#>
#> Descriptive Statistics:
#> ──────────────────────────────────────────────────────────────────────
#> N Mean SD | Median Min Max Skewness Kurtosis
#> ──────────────────────────────────────────────────────────────────────
#> SCH_ID 9679 285.50 164.45 | 285.00 1.00 568.00 -0.00 -1.21
#> SCH_free 9679 2.99 1.86 | 3.00 1.00 7.00 0.47 -0.97
#> SCH_morale 9679 4.02 0.75 | 4.00 2.00 5.00 -0.45 -0.08
#> parent_edu 9679 0.44 0.50 | 0.00 0.00 1.00 0.26 -1.93
#> family_inc 9679 9.26 2.34 | 10.00 1.00 16.00 -0.79 0.72
#> gender* 9679 1.48 0.50 | 1.00 1.00 2.00 0.08 -1.99
#> partjob 9679 0.39 0.49 | 0.00 0.00 1.00 0.47 -1.78
#> attachment 9679 0.89 0.32 | 1.00 0.00 1.00 -2.42 3.87
#> fight 9679 0.13 0.33 | 0.00 0.00 1.00 2.26 3.10
#> late 9679 2.24 1.13 | 2.00 1.00 5.00 0.90 0.29
#> score 9679 51.91 9.69 | 52.00 19.00 87.00 -0.11 -0.12
#> gender01 9679 0.48 0.50 | 0.00 0.00 1.00 0.08 -1.99
#> pass* 9679 1.60 0.49 | 2.00 1.00 2.00 -0.42 -1.83
#> ──────────────────────────────────────────────────────────────────────
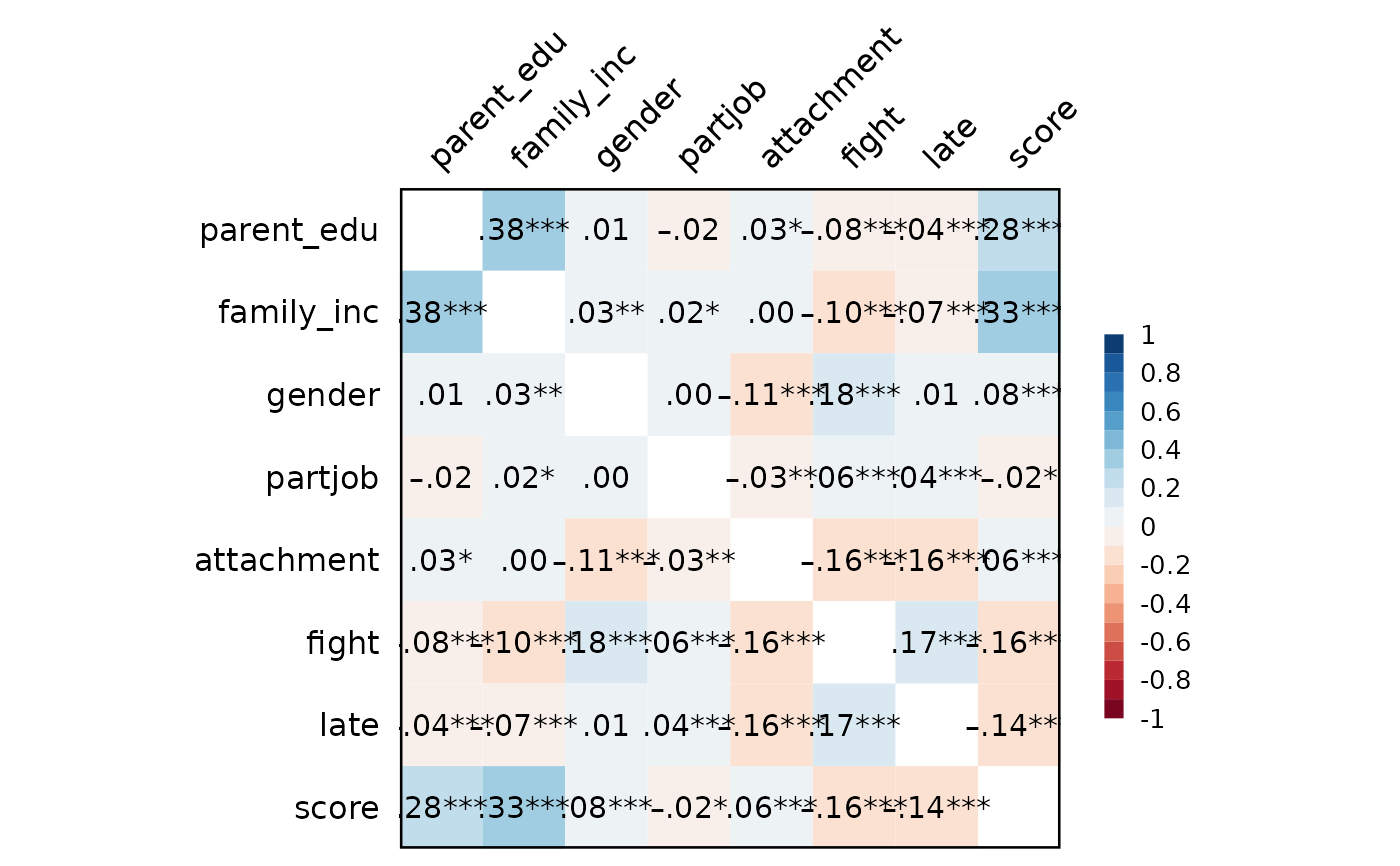
Corr(data[,4:11]) # file="xxx.doc"
#> NOTE: `gender` transformed to numeric.
#>
#> Pearson's r and 95% confidence intervals:
#> ──────────────────────────────────────────────────────────
#> r [95% CI] p N
#> ──────────────────────────────────────────────────────────
#> parent_edu-family_inc 0.38 [ 0.36, 0.40] <.001 *** 9679
#> parent_edu-gender 0.01 [-0.01, 0.03] .320 9679
#> parent_edu-partjob -0.02 [-0.04, 0.00] .071 . 9679
#> parent_edu-attachment 0.03 [ 0.01, 0.05] .012 * 9679
#> parent_edu-fight -0.08 [-0.10, -0.06] <.001 *** 9679
#> parent_edu-late -0.04 [-0.06, -0.02] <.001 *** 9679
#> parent_edu-score 0.28 [ 0.27, 0.30] <.001 *** 9679
#> family_inc-gender 0.03 [ 0.01, 0.05] .008 ** 9679
#> family_inc-partjob 0.02 [ 0.00, 0.04] .044 * 9679
#> family_inc-attachment 0.00 [-0.02, 0.02] .763 9679
#> family_inc-fight -0.10 [-0.12, -0.08] <.001 *** 9679
#> family_inc-late -0.07 [-0.09, -0.05] <.001 *** 9679
#> family_inc-score 0.33 [ 0.32, 0.35] <.001 *** 9679
#> gender-partjob 0.00 [-0.02, 0.02] .842 9679
#> gender-attachment -0.11 [-0.13, -0.09] <.001 *** 9679
#> gender-fight 0.18 [ 0.16, 0.20] <.001 *** 9679
#> gender-late 0.01 [-0.01, 0.03] .582 9679
#> gender-score 0.08 [ 0.06, 0.10] <.001 *** 9679
#> partjob-attachment -0.03 [-0.05, -0.01] .001 ** 9679
#> partjob-fight 0.06 [ 0.04, 0.08] <.001 *** 9679
#> partjob-late 0.04 [ 0.02, 0.06] <.001 *** 9679
#> partjob-score -0.02 [-0.04, -0.00] .047 * 9679
#> attachment-fight -0.16 [-0.18, -0.14] <.001 *** 9679
#> attachment-late -0.16 [-0.18, -0.14] <.001 *** 9679
#> attachment-score 0.06 [ 0.04, 0.08] <.001 *** 9679
#> fight-late 0.17 [ 0.15, 0.18] <.001 *** 9679
#> fight-score -0.16 [-0.18, -0.14] <.001 *** 9679
#> late-score -0.14 [-0.16, -0.12] <.001 *** 9679
#> ──────────────────────────────────────────────────────────
 #### PROCESS Analyses ####
## Model 1 ##
PROCESS(data, y="score", x="late", mods="gender") # continuous Y
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : score
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ late*gender
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ───────────────────────────────────────────
#> (1) score (2) score
#> ───────────────────────────────────────────
#> (Intercept) 51.912 *** 51.174 ***
#> (0.098) (0.135)
#> late -1.174 *** -0.947 ***
#> (0.087) (0.122)
#> genderMale 1.545 ***
#> (0.195)
#> late:genderMale -0.462 **
#> (0.173)
#> ───────────────────────────────────────────
#> R^2 0.019 0.026
#> Adj. R^2 0.018 0.025
#> Num. obs. 9679 9679
#> ───────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "score" (Y)
#> ──────────────────────────────────────
#> F df1 df2 p
#> ──────────────────────────────────────
#> late * gender 7.14 1 9675 .008 **
#> ──────────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "score" (Y)
#> ───────────────────────────────────────────────────────────
#> "gender" Effect S.E. t p [95% CI]
#> ───────────────────────────────────────────────────────────
#> Female -0.947 (0.122) -7.772 <.001 *** [-1.186, -0.708]
#> Male -1.409 (0.122) -11.513 <.001 *** [-1.649, -1.169]
#> ───────────────────────────────────────────────────────────
#>
PROCESS(data, y="pass", x="late", mods="gender") # dichotomous Y
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : pass
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - pass ~ late*gender
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ──────────────────────────────────────────────
#> (1) pass (2) pass
#> ──────────────────────────────────────────────
#> (Intercept) 0.418 *** 0.306 ***
#> (0.021) (0.029)
#> late -0.232 *** -0.201 ***
#> (0.019) (0.026)
#> genderMale 0.238 ***
#> (0.042)
#> late:genderMale -0.066
#> (0.037)
#> ──────────────────────────────────────────────
#> McFadden's R^2 0.012 0.015
#> Nagelkerke's R^2 0.022 0.027
#> AIC 12859.980 12829.489
#> BIC 12874.335 12858.200
#> Num. obs. 9679 9679
#> ──────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "pass" (Y)
#> ─────────────────────────────────
#> Chisq df p
#> ─────────────────────────────────
#> late * gender 3.18 1 .075 .
#> ─────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "pass" (Y)
#> ───────────────────────────────────────────────────────────
#> "gender" Effect S.E. z p [95% CI]
#> ───────────────────────────────────────────────────────────
#> Female -0.201 (0.026) -7.769 <.001 *** [-0.252, -0.151]
#> Male -0.268 (0.027) -10.082 <.001 *** [-0.320, -0.216]
#> ───────────────────────────────────────────────────────────
#>
# (multilevel moderation)
PROCESS(data, y="score", x="late", mods="gender", # continuous Y (LMM)
clusters="SCH_ID")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : score
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : SCH_ID
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ late*gender + (1 | SCH_ID)
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ─────────────────────────────────────────────────────
#> (1) score (2) score
#> ─────────────────────────────────────────────────────
#> (Intercept) 51.705 *** 50.986 ***
#> (0.204) (0.221)
#> late -0.932 *** -0.763 ***
#> (0.082) (0.114)
#> genderMale 1.509 ***
#> (0.182)
#> late:genderMale -0.346 *
#> (0.160)
#> ─────────────────────────────────────────────────────
#> Marginal R^2 0.012 0.018
#> Conditional R^2 0.209 0.214
#> AIC 70092.182 70027.142
#> BIC 70120.893 70070.208
#> Num. obs. 9679 9679
#> Num. groups: SCH_ID 568 568
#> Var: SCH_ID (Intercept) 18.549 18.392
#> Var: Residual 74.298 73.764
#> ─────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "score" (Y)
#> ──────────────────────────────────────
#> F df1 df2 p
#> ──────────────────────────────────────
#> late * gender 4.70 1 9356 .030 *
#> ──────────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "score" (Y)
#> ──────────────────────────────────────────────────────────
#> "gender" Effect S.E. t p [95% CI]
#> ──────────────────────────────────────────────────────────
#> Female -0.763 (0.114) -6.676 <.001 *** [-0.987, -0.539]
#> Male -1.109 (0.114) -9.688 <.001 *** [-1.333, -0.885]
#> ──────────────────────────────────────────────────────────
#>
PROCESS(data, y="pass", x="late", mods="gender", # dichotomous Y (GLMM)
clusters="SCH_ID")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : pass
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : SCH_ID
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - pass ~ late*gender + (1 | SCH_ID)
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ─────────────────────────────────────────────────────
#> (1) pass (2) pass
#> ─────────────────────────────────────────────────────
#> (Intercept) 0.441 *** 0.314 ***
#> (0.044) (0.049)
#> late -0.224 *** -0.202 ***
#> (0.021) (0.029)
#> genderMale 0.271 ***
#> (0.047)
#> late:genderMale -0.049
#> (0.041)
#> ─────────────────────────────────────────────────────
#> AIC 12227.697 12197.299
#> BIC 12249.231 12233.188
#> Num. obs. 9679 9679
#> Num. groups: SCH_ID 568 568
#> Var: SCH_ID (Intercept) 0.754 0.756
#> ─────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "pass" (Y)
#> ─────────────────────────────────
#> Chisq df p
#> ─────────────────────────────────
#> late * gender 1.43 1 .232
#> ─────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "pass" (Y)
#> ──────────────────────────────────────────────────────────
#> "gender" Effect S.E. z p [95% CI]
#> ──────────────────────────────────────────────────────────
#> Female -0.202 (0.029) -6.997 <.001 *** [-0.259, -0.145]
#> Male -0.251 (0.029) -8.541 <.001 *** [-0.308, -0.193]
#> ──────────────────────────────────────────────────────────
#>
# (Johnson-Neyman (J-N) interval and plot)
PROCESS(data, y="score", x="gender", mods="late") -> P
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : score
#> - Predictor (X) : gender (recoded: Female=0, Male=1)
#> - Mediators (M) : -
#> - Moderators (W) : late
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ gender*late
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ───────────────────────────────────────
#> (1) score (2) score
#> ───────────────────────────────────────
#> (Intercept) 51.912 *** 51.913 ***
#> (0.098) (0.097)
#> gender 1.530 *** 1.545 ***
#> (0.196) (0.195)
#> late -1.169 ***
#> (0.086)
#> gender:late -0.462 **
#> (0.173)
#> ───────────────────────────────────────
#> R^2 0.006 0.026
#> Adj. R^2 0.006 0.025
#> Num. obs. 9679 9679
#> ───────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "score" (Y)
#> ──────────────────────────────────────
#> F df1 df2 p
#> ──────────────────────────────────────
#> gender * late 7.14 1 9675 .008 **
#> ──────────────────────────────────────
#>
#> Simple Slopes: "gender" (X) ==> "score" (Y)
#> ───────────────────────────────────────────────────────────
#> "late" Effect S.E. t p [95% CI]
#> ───────────────────────────────────────────────────────────
#> 1.116 (- SD) 2.064 (0.275) 7.504 <.001 *** [1.525, 2.604]
#> 2.242 (Mean) 1.545 (0.195) 7.938 <.001 *** [1.163, 1.926]
#> 3.367 (+ SD) 1.025 (0.275) 3.727 <.001 *** [0.486, 1.564]
#> ───────────────────────────────────────────────────────────
#>
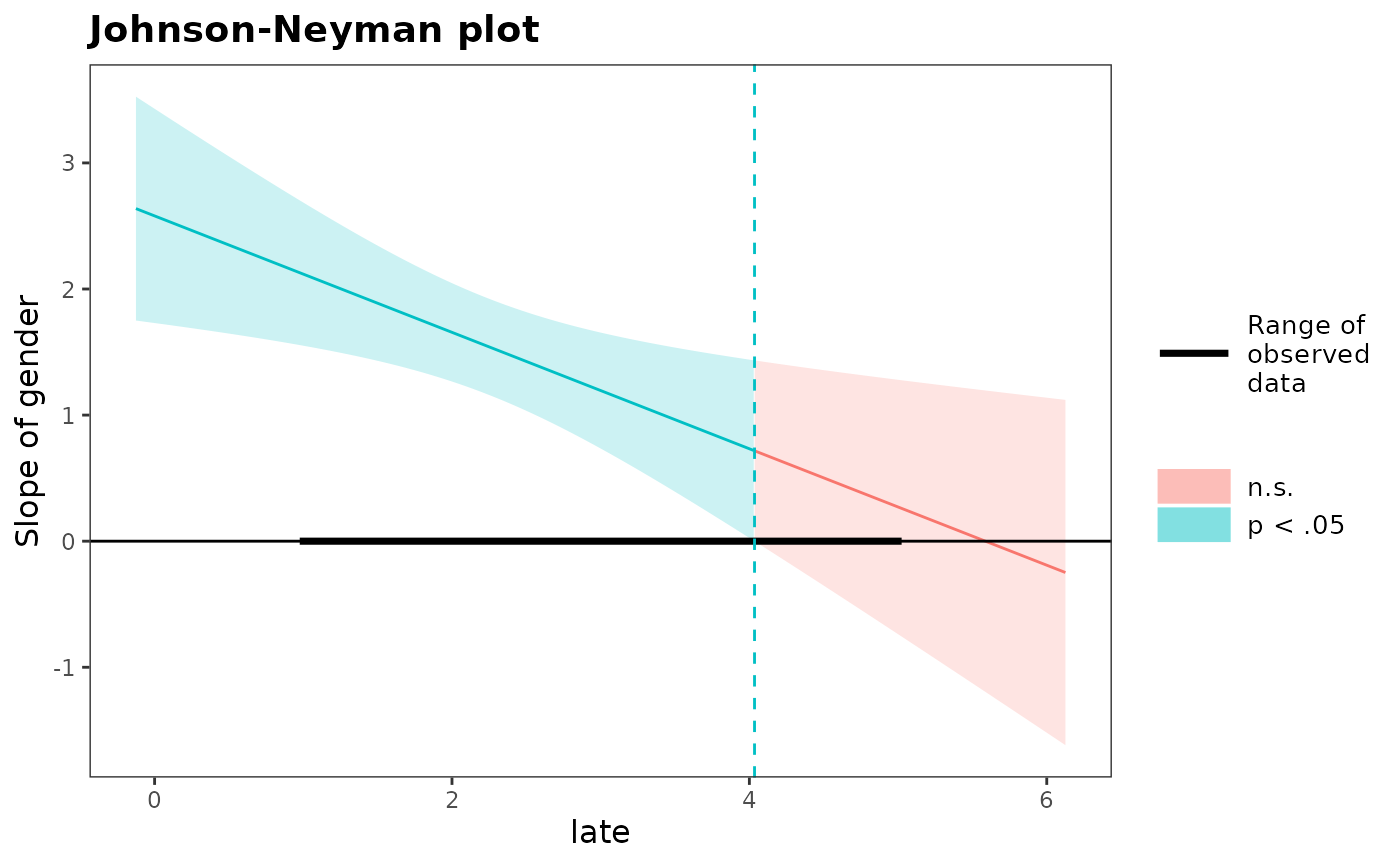
P$results[[1]]$jn[[1]] # Johnson-Neyman interval
#> JOHNSON-NEYMAN INTERVAL
#>
#> When late is OUTSIDE the interval [4.03, 14.93], the slope of gender
#> is p < .05.
#>
#> Note: The range of observed values of late is [1.00, 5.00]
#>
P$results[[1]]$jn[[1]]$plot # Johnson-Neyman plot (ggplot object)
#### PROCESS Analyses ####
## Model 1 ##
PROCESS(data, y="score", x="late", mods="gender") # continuous Y
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : score
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ late*gender
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ───────────────────────────────────────────
#> (1) score (2) score
#> ───────────────────────────────────────────
#> (Intercept) 51.912 *** 51.174 ***
#> (0.098) (0.135)
#> late -1.174 *** -0.947 ***
#> (0.087) (0.122)
#> genderMale 1.545 ***
#> (0.195)
#> late:genderMale -0.462 **
#> (0.173)
#> ───────────────────────────────────────────
#> R^2 0.019 0.026
#> Adj. R^2 0.018 0.025
#> Num. obs. 9679 9679
#> ───────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "score" (Y)
#> ──────────────────────────────────────
#> F df1 df2 p
#> ──────────────────────────────────────
#> late * gender 7.14 1 9675 .008 **
#> ──────────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "score" (Y)
#> ───────────────────────────────────────────────────────────
#> "gender" Effect S.E. t p [95% CI]
#> ───────────────────────────────────────────────────────────
#> Female -0.947 (0.122) -7.772 <.001 *** [-1.186, -0.708]
#> Male -1.409 (0.122) -11.513 <.001 *** [-1.649, -1.169]
#> ───────────────────────────────────────────────────────────
#>
PROCESS(data, y="pass", x="late", mods="gender") # dichotomous Y
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : pass
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - pass ~ late*gender
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ──────────────────────────────────────────────
#> (1) pass (2) pass
#> ──────────────────────────────────────────────
#> (Intercept) 0.418 *** 0.306 ***
#> (0.021) (0.029)
#> late -0.232 *** -0.201 ***
#> (0.019) (0.026)
#> genderMale 0.238 ***
#> (0.042)
#> late:genderMale -0.066
#> (0.037)
#> ──────────────────────────────────────────────
#> McFadden's R^2 0.012 0.015
#> Nagelkerke's R^2 0.022 0.027
#> AIC 12859.980 12829.489
#> BIC 12874.335 12858.200
#> Num. obs. 9679 9679
#> ──────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "pass" (Y)
#> ─────────────────────────────────
#> Chisq df p
#> ─────────────────────────────────
#> late * gender 3.18 1 .075 .
#> ─────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "pass" (Y)
#> ───────────────────────────────────────────────────────────
#> "gender" Effect S.E. z p [95% CI]
#> ───────────────────────────────────────────────────────────
#> Female -0.201 (0.026) -7.769 <.001 *** [-0.252, -0.151]
#> Male -0.268 (0.027) -10.082 <.001 *** [-0.320, -0.216]
#> ───────────────────────────────────────────────────────────
#>
# (multilevel moderation)
PROCESS(data, y="score", x="late", mods="gender", # continuous Y (LMM)
clusters="SCH_ID")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : score
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : SCH_ID
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ late*gender + (1 | SCH_ID)
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ─────────────────────────────────────────────────────
#> (1) score (2) score
#> ─────────────────────────────────────────────────────
#> (Intercept) 51.705 *** 50.986 ***
#> (0.204) (0.221)
#> late -0.932 *** -0.763 ***
#> (0.082) (0.114)
#> genderMale 1.509 ***
#> (0.182)
#> late:genderMale -0.346 *
#> (0.160)
#> ─────────────────────────────────────────────────────
#> Marginal R^2 0.012 0.018
#> Conditional R^2 0.209 0.214
#> AIC 70092.182 70027.142
#> BIC 70120.893 70070.208
#> Num. obs. 9679 9679
#> Num. groups: SCH_ID 568 568
#> Var: SCH_ID (Intercept) 18.549 18.392
#> Var: Residual 74.298 73.764
#> ─────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "score" (Y)
#> ──────────────────────────────────────
#> F df1 df2 p
#> ──────────────────────────────────────
#> late * gender 4.70 1 9356 .030 *
#> ──────────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "score" (Y)
#> ──────────────────────────────────────────────────────────
#> "gender" Effect S.E. t p [95% CI]
#> ──────────────────────────────────────────────────────────
#> Female -0.763 (0.114) -6.676 <.001 *** [-0.987, -0.539]
#> Male -1.109 (0.114) -9.688 <.001 *** [-1.333, -0.885]
#> ──────────────────────────────────────────────────────────
#>
PROCESS(data, y="pass", x="late", mods="gender", # dichotomous Y (GLMM)
clusters="SCH_ID")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : pass
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : SCH_ID
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - pass ~ late*gender + (1 | SCH_ID)
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ─────────────────────────────────────────────────────
#> (1) pass (2) pass
#> ─────────────────────────────────────────────────────
#> (Intercept) 0.441 *** 0.314 ***
#> (0.044) (0.049)
#> late -0.224 *** -0.202 ***
#> (0.021) (0.029)
#> genderMale 0.271 ***
#> (0.047)
#> late:genderMale -0.049
#> (0.041)
#> ─────────────────────────────────────────────────────
#> AIC 12227.697 12197.299
#> BIC 12249.231 12233.188
#> Num. obs. 9679 9679
#> Num. groups: SCH_ID 568 568
#> Var: SCH_ID (Intercept) 0.754 0.756
#> ─────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "pass" (Y)
#> ─────────────────────────────────
#> Chisq df p
#> ─────────────────────────────────
#> late * gender 1.43 1 .232
#> ─────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "pass" (Y)
#> ──────────────────────────────────────────────────────────
#> "gender" Effect S.E. z p [95% CI]
#> ──────────────────────────────────────────────────────────
#> Female -0.202 (0.029) -6.997 <.001 *** [-0.259, -0.145]
#> Male -0.251 (0.029) -8.541 <.001 *** [-0.308, -0.193]
#> ──────────────────────────────────────────────────────────
#>
# (Johnson-Neyman (J-N) interval and plot)
PROCESS(data, y="score", x="gender", mods="late") -> P
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : score
#> - Predictor (X) : gender (recoded: Female=0, Male=1)
#> - Mediators (M) : -
#> - Moderators (W) : late
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ gender*late
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ───────────────────────────────────────
#> (1) score (2) score
#> ───────────────────────────────────────
#> (Intercept) 51.912 *** 51.913 ***
#> (0.098) (0.097)
#> gender 1.530 *** 1.545 ***
#> (0.196) (0.195)
#> late -1.169 ***
#> (0.086)
#> gender:late -0.462 **
#> (0.173)
#> ───────────────────────────────────────
#> R^2 0.006 0.026
#> Adj. R^2 0.006 0.025
#> Num. obs. 9679 9679
#> ───────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "score" (Y)
#> ──────────────────────────────────────
#> F df1 df2 p
#> ──────────────────────────────────────
#> gender * late 7.14 1 9675 .008 **
#> ──────────────────────────────────────
#>
#> Simple Slopes: "gender" (X) ==> "score" (Y)
#> ───────────────────────────────────────────────────────────
#> "late" Effect S.E. t p [95% CI]
#> ───────────────────────────────────────────────────────────
#> 1.116 (- SD) 2.064 (0.275) 7.504 <.001 *** [1.525, 2.604]
#> 2.242 (Mean) 1.545 (0.195) 7.938 <.001 *** [1.163, 1.926]
#> 3.367 (+ SD) 1.025 (0.275) 3.727 <.001 *** [0.486, 1.564]
#> ───────────────────────────────────────────────────────────
#>
P$results[[1]]$jn[[1]] # Johnson-Neyman interval
#> JOHNSON-NEYMAN INTERVAL
#>
#> When late is OUTSIDE the interval [4.03, 14.93], the slope of gender
#> is p < .05.
#>
#> Note: The range of observed values of late is [1.00, 5.00]
#>
P$results[[1]]$jn[[1]]$plot # Johnson-Neyman plot (ggplot object)
 GLM_summary(P$model.y) # detailed results of regression
#>
#> General Linear Model (OLS Regression)
#>
#> Model Fit:
#> F(3, 9675) = 84.92, p = 3e-54 ***
#> R² = 0.02566 (Adjusted R² = 0.02535)
#>
#> Unstandardized Coefficients:
#> Outcome Variable: score
#> N = 9679
#> ────────────────────────────────────────────────────────────────────
#> b S.E. t p [95% CI of b] VIF
#> ────────────────────────────────────────────────────────────────────
#> (Intercept) 51.913 (0.097) 534.035 <.001 *** [51.723, 52.104]
#> gender 1.545 (0.195) 7.938 <.001 *** [ 1.163, 1.926] 1.000
#> late -1.169 (0.086) -13.519 <.001 *** [-1.338, -0.999] 1.001
#> gender:late -0.462 (0.173) -2.673 .008 ** [-0.800, -0.123] 1.001
#> ────────────────────────────────────────────────────────────────────
#>
#> Standardized Coefficients (β):
#> Outcome Variable: score
#> N = 9679
#> ─────────────────────────────────────────────────────────────────────────────────
#> β S.E. t p [95% CI of β] r(partial) r(part)
#> ─────────────────────────────────────────────────────────────────────────────────
#> gender 0.080 (0.010) 7.938 <.001 *** [ 0.060, 0.099] 0.080 0.080
#> late -0.136 (0.010) -13.519 <.001 *** [-0.155, -0.116] -0.136 -0.136
#> gender:late -0.027 (0.010) -2.673 .008 ** [-0.047, -0.007] -0.027 -0.027
#> ─────────────────────────────────────────────────────────────────────────────────
#>
# (allows multicategorical moderator)
d = airquality
d$Month = as.factor(d$Month) # moderator: factor with levels "5"~"9"
PROCESS(d, y="Temp", x="Solar.R", mods="Month")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : Temp
#> - Predictor (X) : Solar.R
#> - Mediators (M) : -
#> - Moderators (W) : Month
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - Temp ~ Solar.R*Month
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ────────────────────────────────────────
#> (1) Temp (2) Temp
#> ────────────────────────────────────────
#> (Intercept) 78.116 *** 66.012 ***
#> (0.736) (1.232)
#> Solar.R 0.028 *** 0.027 *
#> (0.008) (0.011)
#> Month6 12.967 ***
#> (1.699)
#> Month7 17.366 ***
#> (1.742)
#> Month8 18.235 ***
#> (1.741)
#> Month9 11.129 ***
#> (1.721)
#> Solar.R:Month6 0.002
#> (0.017)
#> Solar.R:Month7 -0.009
#> (0.018)
#> Solar.R:Month8 0.009
#> (0.019)
#> Solar.R:Month9 -0.014
#> (0.019)
#> ────────────────────────────────────────
#> R^2 0.076 0.549
#> Adj. R^2 0.070 0.519
#> Num. obs. 146 146
#> ────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 146 (7 missing observations deleted)
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "Temp" (Y)
#> ───────────────────────────────────────
#> F df1 df2 p
#> ───────────────────────────────────────
#> Solar.R * Month 0.36 4 136 .838
#> ───────────────────────────────────────
#>
#> Simple Slopes: "Solar.R" (X) ==> "Temp" (Y)
#> ───────────────────────────────────────────────────────
#> "Month" Effect S.E. t p [95% CI]
#> ───────────────────────────────────────────────────────
#> 5 0.027 (0.011) 2.432 .016 * [ 0.005, 0.048]
#> 6 0.029 (0.013) 2.242 .027 * [ 0.003, 0.054]
#> 7 0.017 (0.014) 1.186 .238 [-0.011, 0.046]
#> 8 0.035 (0.016) 2.202 .029 * [ 0.004, 0.067]
#> 9 0.013 (0.015) 0.865 .389 [-0.017, 0.043]
#> ───────────────────────────────────────────────────────
#>
## Model 2 ##
PROCESS(data, y="score", x="late",
mods=c("gender", "family_inc"),
mod.type="2-way") # or omit "mod.type", default is "2-way"
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 2
#> Model Type : Parallel Moderation (2 mods; 2-way)
#> - Outcome (Y) : score
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender, family_inc
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ late*gender + late*family_inc
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ───────────────────────────────────────────
#> (1) score (2) score
#> ───────────────────────────────────────────
#> (Intercept) 51.912 *** 51.255 ***
#> (0.098) (0.127)
#> late -1.174 *** -0.836 ***
#> (0.087) (0.115)
#> genderMale 1.375 ***
#> (0.184)
#> family_inc 1.339 ***
#> (0.040)
#> late:genderMale -0.301
#> (0.163)
#> late:family_inc 0.007
#> (0.034)
#> ───────────────────────────────────────────
#> R^2 0.019 0.129
#> Adj. R^2 0.018 0.129
#> Num. obs. 9679 9679
#> ───────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Parallel Moderation (2 mods; 2-way) (Model 2)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effects on "score" (Y)
#> ───────────────────────────────────────────
#> F df1 df2 p
#> ───────────────────────────────────────────
#> late * gender 3.40 1 9673 .065 .
#> late * family_inc 0.04 1 9673 .849
#> (All Interactions) 1.72 2 9673 .179
#> ───────────────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "score" (Y)
#> ────────────────────────────────────────────────────────────────────────
#> "family_inc" "gender" Effect S.E. t p [95% CI]
#> ────────────────────────────────────────────────────────────────────────
#> 6.923 (- SD) Female -0.851 (0.137) -6.219 <.001 *** [-1.119, -0.583]
#> 6.923 (- SD) Male -1.152 (0.138) -8.369 <.001 *** [-1.422, -0.882]
#> 9.258 (Mean) Female -0.836 (0.115) -7.238 <.001 *** [-1.062, -0.609]
#> 9.258 (Mean) Male -1.137 (0.116) -9.792 <.001 *** [-1.365, -0.909]
#> 11.594 (+ SD) Female -0.820 (0.144) -5.699 <.001 *** [-1.103, -0.538]
#> 11.594 (+ SD) Male -1.122 (0.144) -7.778 <.001 *** [-1.405, -0.839]
#> ────────────────────────────────────────────────────────────────────────
#>
## Model 3 ##
PROCESS(data, y="score", x="late",
mods=c("gender", "family_inc"),
mod.type="3-way")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 3
#> Model Type : Moderated Moderation (2 mods; 3-way)
#> - Outcome (Y) : score
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender, family_inc
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ late*gender*family_inc
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ──────────────────────────────────────────────────────
#> (1) score (2) score
#> ──────────────────────────────────────────────────────
#> (Intercept) 51.912 *** 51.266 ***
#> (0.098) (0.127)
#> late -1.174 *** -0.818 ***
#> (0.087) (0.116)
#> genderMale 1.348 ***
#> (0.185)
#> family_inc 1.375 ***
#> (0.055)
#> late:genderMale -0.339 *
#> (0.164)
#> late:family_inc 0.088
#> (0.050)
#> genderMale:family_inc -0.069
#> (0.079)
#> late:genderMale:family_inc -0.153 *
#> (0.069)
#> ──────────────────────────────────────────────────────
#> R^2 0.019 0.130
#> Adj. R^2 0.018 0.129
#> Num. obs. 9679 9679
#> ──────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Moderated Moderation (2 mods; 3-way) (Model 3)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effects on "score" (Y)
#> ───────────────────────────────────────────────────
#> F df1 df2 p
#> ───────────────────────────────────────────────────
#> late * gender 4.26 1 9671 .039 *
#> late * family_inc 3.11 1 9671 .078 .
#> gender * family_inc 0.75 1 9671 .386
#> late * gender * family_inc 4.95 1 9671 .026 *
#> (All Interactions) 2.33 4 9671 .054 .
#> ───────────────────────────────────────────────────
#>
#> Conditional Interaction Effects on "score" (Y)
#> ────────────────────────────────────────────────────
#> "family_inc" Interaction F df1 df2 p
#> ────────────────────────────────────────────────────
#> 6.923 (- SD) late * gender 0.01 1 9671 .938
#> 9.258 (Mean) late * gender 4.26 1 9671 .039 *
#> 11.594 (+ SD) late * gender 8.56 1 9671 .003 **
#> ────────────────────────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "score" (Y)
#> ────────────────────────────────────────────────────────────────────────
#> "family_inc" "gender" Effect S.E. t p [95% CI]
#> ────────────────────────────────────────────────────────────────────────
#> 6.923 (- SD) Female -1.022 (0.157) -6.506 <.001 *** [-1.330, -0.714]
#> 6.923 (- SD) Male -1.005 (0.155) -6.470 <.001 *** [-1.309, -0.700]
#> 9.258 (Mean) Female -0.818 (0.116) -7.068 <.001 *** [-1.044, -0.591]
#> 9.258 (Mean) Male -1.157 (0.117) -9.927 <.001 *** [-1.385, -0.928]
#> 11.594 (+ SD) Female -0.613 (0.170) -3.604 <.001 *** [-0.947, -0.280]
#> 11.594 (+ SD) Male -1.308 (0.166) -7.894 <.001 *** [-1.633, -0.983]
#> ────────────────────────────────────────────────────────────────────────
#>
PROCESS(data, y="pass", x="gender",
mods=c("late", "family_inc"),
mod1.val=c(1, 3, 5), # moderator 1: late
mod2.val=seq(1, 15, 2), # moderator 2: family_inc
mod.type="3-way")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 3
#> Model Type : Moderated Moderation (2 mods; 3-way)
#> - Outcome (Y) : pass
#> - Predictor (X) : gender (recoded: Female=0, Male=1)
#> - Mediators (M) : -
#> - Moderators (W) : late, family_inc
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - pass ~ gender*late*family_inc
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ────────────────────────────────────────────────────
#> (1) pass (2) pass
#> ────────────────────────────────────────────────────
#> (Intercept) 0.414 *** 0.442 ***
#> (0.021) (0.022)
#> gender 0.228 *** 0.219 ***
#> (0.042) (0.044)
#> late -0.216 ***
#> (0.019)
#> family_inc 0.259 ***
#> (0.010)
#> gender:late -0.046
#> (0.039)
#> gender:family_inc -0.022
#> (0.020)
#> late:family_inc 0.005
#> (0.009)
#> gender:late:family_inc -0.032
#> (0.018)
#> ────────────────────────────────────────────────────
#> McFadden's R^2 0.002 0.073
#> Nagelkerke's R^2 0.004 0.127
#> AIC 12989.483 12080.387
#> BIC 13003.839 12137.809
#> Num. obs. 9679 9679
#> ────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Moderated Moderation (2 mods; 3-way) (Model 3)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effects on "pass" (Y)
#> ──────────────────────────────────────────────
#> Chisq df p
#> ──────────────────────────────────────────────
#> gender * late 1.43 1 .231
#> gender * family_inc 1.17 1 .279
#> late * family_inc 0.32 1 .573
#> gender * late * family_inc 3.18 1 .075 .
#> (All Interactions) 5.72 4 .221
#> ──────────────────────────────────────────────
#>
#> Conditional Interaction Effects on "pass" (Y)
#> ──────────────────────────────────────────────
#> "family_inc" Interaction Chisq df p
#> ──────────────────────────────────────────────
#> 1.000 gender * late 2.08 1 .149
#> 3.000 gender * late 1.73 1 .188
#> 5.000 gender * late 1.15 1 .285
#> 7.000 gender * late 0.22 1 .642
#> 9.000 gender * late 0.97 1 .323
#> 11.000 gender * late 3.93 1 .047 *
#> 13.000 gender * late 4.34 1 .037 *
#> 15.000 gender * late 4.19 1 .041 *
#> ──────────────────────────────────────────────
#>
#> Simple Slopes: "gender" (X) ==> "pass" (Y)
#> ────────────────────────────────────────────────────────────────────
#> "family_inc" "late" Effect S.E. z p [95% CI]
#> ────────────────────────────────────────────────────────────────────
#> 1.000 1.000 0.131 (0.253) 0.518 .605 [-0.365, 0.627]
#> 1.000 3.000 0.561 (0.201) 2.795 .005 ** [ 0.168, 0.954]
#> 1.000 5.000 0.991 (0.441) 2.247 .025 * [ 0.127, 1.855]
#> 3.000 1.000 0.166 (0.196) 0.850 .395 [-0.217, 0.550]
#> 3.000 3.000 0.470 (0.155) 3.029 .002 ** [ 0.166, 0.774]
#> 3.000 5.000 0.773 (0.341) 2.270 .023 * [ 0.106, 1.440]
#> 5.000 1.000 0.202 (0.141) 1.435 .151 [-0.074, 0.477]
#> 5.000 3.000 0.378 (0.111) 3.402 <.001 *** [ 0.160, 0.596]
#> 5.000 5.000 0.555 (0.244) 2.275 .023 * [ 0.077, 1.033]
#> 7.000 1.000 0.237 (0.092) 2.576 .010 ** [ 0.057, 0.418]
#> 7.000 3.000 0.287 (0.072) 3.962 <.001 *** [ 0.145, 0.429]
#> 7.000 5.000 0.337 (0.159) 2.124 .034 * [ 0.026, 0.649]
#> 9.000 1.000 0.272 (0.066) 4.109 <.001 *** [ 0.143, 0.402]
#> 9.000 3.000 0.196 (0.052) 3.775 <.001 *** [ 0.094, 0.298]
#> 9.000 5.000 0.120 (0.114) 1.049 .294 [-0.104, 0.343]
#> 11.000 1.000 0.308 (0.087) 3.544 <.001 *** [ 0.138, 0.478]
#> 11.000 3.000 0.105 (0.069) 1.529 .126 [-0.030, 0.239]
#> 11.000 5.000 -0.098 (0.151) -0.650 .515 [-0.395, 0.198]
#> 13.000 1.000 0.343 (0.134) 2.564 .010 * [ 0.081, 0.606]
#> 13.000 3.000 0.014 (0.106) 0.128 .898 [-0.194, 0.221]
#> 13.000 5.000 -0.316 (0.234) -1.351 .177 [-0.775, 0.143]
#> 15.000 1.000 0.379 (0.188) 2.009 .045 * [ 0.009, 0.748]
#> 15.000 3.000 -0.078 (0.150) -0.520 .603 [-0.371, 0.215]
#> 15.000 5.000 -0.534 (0.330) -1.619 .105 [-1.181, 0.113]
#> ────────────────────────────────────────────────────────────────────
#>
## Model 4 ##
PROCESS(data, y="score", x="parent_edu",
meds="family_inc", covs="gender",
ci="boot", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 4
#> Model Type : Simple Mediation
#> - Outcome (Y) : score
#> - Predictor (X) : parent_edu
#> - Mediators (M) : family_inc
#> - Moderators (W) : -
#> - Covariates (C) : gender
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - family_inc ~ gender + parent_edu
#> Formula of Outcome:
#> - score ~ gender + parent_edu + family_inc
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ───────────────────────────────────────────────────────
#> (1) score (2) family_inc (3) score
#> ───────────────────────────────────────────────────────
#> (Intercept) 51.206 *** 9.207 *** 51.262 ***
#> (0.130) (0.030) (0.126)
#> genderMale 1.474 *** 0.108 * 1.358 ***
#> (0.188) (0.044) (0.182)
#> parent_edu 5.537 *** 1.793 *** 3.594 ***
#> (0.190) (0.044) (0.199)
#> family_inc 1.083 ***
#> (0.042)
#> ───────────────────────────────────────────────────────
#> R^2 0.087 0.146 0.145
#> Adj. R^2 0.086 0.146 0.145
#> Num. obs. 9679 9679 9679
#> ───────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘mediation’ (v4.5.1)
#> Effect Type : Simple Mediation (Model 4)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Bootstrap)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Running 100 simulations...
#> Indirect Path: "parent_edu" (X) ==> "family_inc" (M) ==> "score" (Y)
#> ─────────────────────────────────────────────────────────────
#> Effect S.E. z p [Boot 95% CI]
#> ─────────────────────────────────────────────────────────────
#> Indirect (ab) 1.943 (0.089) 21.759 <.001 *** [1.752, 2.095]
#> Direct (c') 3.594 (0.220) 16.319 <.001 *** [3.155, 3.981]
#> Total (c) 5.537 (0.203) 27.249 <.001 *** [5.084, 5.898]
#> ─────────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
# (allows an infinite number of multiple mediators in parallel)
PROCESS(data, y="score", x="parent_edu",
meds=c("family_inc", "late"),
covs=c("gender", "partjob"),
ci="boot", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 4
#> Model Type : Parallel Multiple Mediation (2 meds)
#> - Outcome (Y) : score
#> - Predictor (X) : parent_edu
#> - Mediators (M) : family_inc, late
#> - Moderators (W) : -
#> - Covariates (C) : gender, partjob
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - family_inc ~ gender + partjob + parent_edu
#> - late ~ gender + partjob + parent_edu
#> Formula of Outcome:
#> - score ~ gender + partjob + parent_edu + family_inc + late
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ─────────────────────────────────────────────────────────────────────
#> (1) score (2) family_inc (3) late (4) score
#> ─────────────────────────────────────────────────────────────────────
#> (Intercept) 51.206 *** 9.207 *** 2.235 *** 51.254 ***
#> (0.130) (0.030) (0.016) (0.125)
#> genderMale 1.475 *** 0.107 * 0.013 1.374 ***
#> (0.188) (0.044) (0.023) (0.181)
#> partjob -0.301 0.132 ** 0.091 *** -0.353
#> (0.193) (0.045) (0.023) (0.186)
#> parent_edu 5.531 *** 1.796 *** -0.092 *** 3.545 ***
#> (0.190) (0.044) (0.023) (0.197)
#> family_inc 1.057 ***
#> (0.042)
#> late -0.957 ***
#> (0.081)
#> ─────────────────────────────────────────────────────────────────────
#> R^2 0.087 0.146 0.003 0.158
#> Adj. R^2 0.087 0.146 0.003 0.157
#> Num. obs. 9679 9679 9679 9679
#> ─────────────────────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘mediation’ (v4.5.1)
#> Effect Type : Parallel Multiple Mediation (2 meds) (Model 4)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Bootstrap)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Running 100 simulations...
#> Indirect Path: "parent_edu" (X) ==> "family_inc" (M) ==> "score" (Y)
#> ─────────────────────────────────────────────────────────────
#> Effect S.E. z p [Boot 95% CI]
#> ─────────────────────────────────────────────────────────────
#> Indirect (ab) 1.898 (0.089) 21.262 <.001 *** [1.711, 2.055]
#> Direct (c') 3.545 (0.218) 16.280 <.001 *** [3.089, 3.937]
#> ─────────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Running 100 simulations...
#> Indirect Path: "parent_edu" (X) ==> "late" (M) ==> "score" (Y)
#> ─────────────────────────────────────────────────────────────
#> Effect S.E. z p [Boot 95% CI]
#> ─────────────────────────────────────────────────────────────
#> Indirect (ab) 0.088 (0.022) 3.946 <.001 *** [0.054, 0.136]
#> Direct (c') 3.545 (0.218) 16.280 <.001 *** [3.089, 3.937]
#> ─────────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
# (multilevel mediation)
PROCESS(data, y="score", x="SCH_free",
meds="late", clusters="SCH_ID",
ci="mcmc", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 4
#> Model Type : Simple Mediation
#> - Outcome (Y) : score
#> - Predictor (X) : SCH_free
#> - Mediators (M) : late
#> - Moderators (W) : -
#> - Covariates (C) : -
#> - HLM Clusters : SCH_ID
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - late ~ SCH_free + (1 | SCH_ID)
#> Formula of Outcome:
#> - score ~ SCH_free + late + (1 | SCH_ID)
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ────────────────────────────────────────────────────────────────────
#> (1) score (2) late (3) score
#> ────────────────────────────────────────────────────────────────────
#> (Intercept) 51.853 *** 2.245 *** 51.858 ***
#> (0.162) (0.017) (0.159)
#> SCH_free -1.611 *** 0.049 *** -1.566 ***
#> (0.085) (0.009) (0.084)
#> late -0.902 ***
#> (0.082)
#> ────────────────────────────────────────────────────────────────────
#> Marginal R^2 0.095 0.007 0.106
#> Conditional R^2 0.201 0.073 0.208
#> AIC 69944.810 29498.368 69828.530
#> BIC 69973.521 29527.079 69864.419
#> Num. obs. 9679 9679 9679
#> Num. groups: SCH_ID 568 568 568
#> Var: SCH_ID (Intercept) 9.935 0.084 9.592
#> Var: Residual 75.201 1.176 74.339
#> ────────────────────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘mediation’ (v4.5.1)
#> Effect Type : Simple Mediation (Model 4)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Monte Carlo)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Running 100 simulations...
#> Indirect Path: "SCH_free" (X) ==> "late" (M) ==> "score" (Y)
#> ────────────────────────────────────────────────────────────────
#> Effect S.E. z p [MCMC 95% CI]
#> ────────────────────────────────────────────────────────────────
#> Indirect (ab) -0.044 (0.009) -5.155 <.001 *** [-0.061, -0.030]
#> Direct (c') -1.573 (0.078) -20.230 <.001 *** [-1.720, -1.440]
#> Total (c) -1.618 (0.078) -20.624 <.001 *** [-1.769, -1.480]
#> ────────────────────────────────────────────────────────────────
#> Monte Carlo (Quasi-Bayesian) Confidence Interval
#> (Effect, SE, and CI are estimated based on 100 Monte Carlo samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
## Model 6 ##
PROCESS(data, y="score", x="parent_edu",
meds=c("family_inc", "late"),
covs=c("gender", "partjob"),
med.type="serial",
ci="boot", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 6
#> Model Type : Serial Multiple Mediation (2 meds)
#> - Outcome (Y) : score
#> - Predictor (X) : parent_edu
#> - Mediators (M) : family_inc, late
#> - Moderators (W) : -
#> - Covariates (C) : gender, partjob
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - family_inc ~ gender + partjob + parent_edu
#> - late ~ gender + partjob + parent_edu + family_inc
#> Formula of Outcome:
#> - score ~ gender + partjob + parent_edu + family_inc + late
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ─────────────────────────────────────────────────────────────────────
#> (1) score (2) family_inc (3) late (4) score
#> ─────────────────────────────────────────────────────────────────────
#> (Intercept) 51.206 *** 9.207 *** 2.516 *** 51.254 ***
#> (0.130) (0.030) (0.051) (0.125)
#> genderMale 1.475 *** 0.107 * 0.017 1.374 ***
#> (0.188) (0.044) (0.023) (0.181)
#> partjob -0.301 0.132 ** 0.096 *** -0.353
#> (0.193) (0.045) (0.023) (0.186)
#> parent_edu 5.531 *** 1.796 *** -0.037 3.545 ***
#> (0.190) (0.044) (0.025) (0.197)
#> family_inc -0.030 *** 1.057 ***
#> (0.005) (0.042)
#> late -0.957 ***
#> (0.081)
#> ─────────────────────────────────────────────────────────────────────
#> R^2 0.087 0.146 0.007 0.158
#> Adj. R^2 0.087 0.146 0.006 0.157
#> Num. obs. 9679 9679 9679 9679
#> ─────────────────────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘lavaan’ (v0.6.21)
#> Effect Type : Serial Multiple Mediation (2 meds) (Model 6)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Bootstrap)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Running 100 simulations (lavaan model)...
#> LAVAAN Syntax:
#> family_inc ~ gender + partjob + a1*parent_edu
#> late ~ gender + partjob + a2*parent_edu + d12*family_inc
#> score ~ gender + partjob + c.*parent_edu + b1*family_inc + b2*late
#> Indirect_All := a1*b1 + a2*b2 + a1*d12*b2
#> Ind_X_M1_Y := a1*b1
#> Ind_X_M2_Y := a2*b2
#> Ind_X_M1_M2_Y := a1*d12*b2
#> Direct := c.
#> Total := c. + a1*b1 + a2*b2 + a1*d12*b2
#> ────────────────────────────────────────────────────────────────────────
#> Estimate S.E. z p [Boot 95% CI] Beta
#> ────────────────────────────────────────────────────────────────────────
#> Indirect_All 1.986 (0.088) 22.644 <.001 *** [ 1.798, 2.135] 0.102
#> Ind_X_M1_Y 1.898 (0.083) 22.816 <.001 *** [ 1.724, 2.058] 0.097
#> Ind_X_M2_Y 0.036 (0.027) 1.327 .185 [-0.011, 0.086] 0.002
#> Ind_X_M1_M2_Y 0.052 (0.011) 4.774 <.001 *** [ 0.034, 0.078] 0.003
#> Direct 3.545 (0.178) 19.879 <.001 *** [ 3.179, 3.825] 0.182
#> Total 5.531 (0.171) 32.290 <.001 *** [ 5.130, 5.857] 0.283
#> ────────────────────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
## Model 8 ##
PROCESS(data, y="score", x="fight",
meds="late",
mods="gender",
mod.path=c("x-m", "x-y"),
ci="boot", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 8
#> Model Type : Moderated Mediation
#> - Outcome (Y) : score
#> - Predictor (X) : fight
#> - Mediators (M) : late
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - late ~ fight*gender
#> Formula of Outcome:
#> - score ~ fight*gender + late
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ──────────────────────────────────────────────────────────
#> (1) score (2) late (3) score
#> ──────────────────────────────────────────────────────────
#> (Intercept) 51.912 *** 2.272 *** 50.824 ***
#> (0.097) (0.016) (0.136)
#> fight -4.585 *** 0.646 *** -6.188 ***
#> (0.293) (0.062) (0.527)
#> genderMale -0.057 * 2.129 ***
#> (0.023) (0.196)
#> fight:genderMale -0.103 2.305 ***
#> (0.074) (0.633)
#> late -0.950 ***
#> (0.087)
#> ──────────────────────────────────────────────────────────
#> R^2 0.025 0.028 0.050
#> Adj. R^2 0.025 0.028 0.049
#> Num. obs. 9679 9679 9679
#> ──────────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘mediation’ (v4.5.1), ‘interactions’ (v1.2.0)
#> Effect Type : Moderated Mediation (Model 8)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Bootstrap)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Interaction Effect on "score" (Y)
#> ────────────────────────────────────────
#> F df1 df2 p
#> ────────────────────────────────────────
#> fight * gender 13.24 1 9674 <.001 ***
#> ────────────────────────────────────────
#>
#> Simple Slopes: "fight" (X) ==> "score" (Y)
#> (Conditional Direct Effects [c'] of X on Y)
#> ───────────────────────────────────────────────────────────
#> "gender" Effect S.E. t p [95% CI]
#> ───────────────────────────────────────────────────────────
#> Female -6.188 (0.527) -11.742 <.001 *** [-7.221, -5.155]
#> Male -3.883 (0.359) -10.821 <.001 *** [-4.587, -3.180]
#> ───────────────────────────────────────────────────────────
#>
#> Interaction Effect on "late" (M)
#> ───────────────────────────────────────
#> F df1 df2 p
#> ───────────────────────────────────────
#> fight * gender 1.90 1 9675 .168
#> ───────────────────────────────────────
#>
#> Simple Slopes: "fight" (X) ==> "late" (M)
#> (Conditional Effects [a] of X on M)
#> ────────────────────────────────────────────────────────
#> "gender" Effect S.E. t p [95% CI]
#> ────────────────────────────────────────────────────────
#> Female 0.646 (0.062) 10.485 <.001 *** [0.525, 0.766]
#> Male 0.543 (0.042) 12.989 <.001 *** [0.461, 0.625]
#> ────────────────────────────────────────────────────────
#>
#> Running 100 * 2 simulations...
#> Indirect Path: "fight" (X) ==> "late" (M) ==> "score" (Y)
#> (Conditional Indirect Effects [ab] of X through M on Y)
#> ──────────────────────────────────────────────────────────
#> "gender" Effect S.E. z p [Boot 95% CI]
#> ──────────────────────────────────────────────────────────
#> Female -0.614 (0.086) -7.117 <.001 *** [-0.807, -0.477]
#> Male -0.516 (0.060) -8.538 <.001 *** [-0.645, -0.411]
#> ──────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
## For more examples and details, see:
## https://github.com/psychbruce/bruceR/tree/main/note
GLM_summary(P$model.y) # detailed results of regression
#>
#> General Linear Model (OLS Regression)
#>
#> Model Fit:
#> F(3, 9675) = 84.92, p = 3e-54 ***
#> R² = 0.02566 (Adjusted R² = 0.02535)
#>
#> Unstandardized Coefficients:
#> Outcome Variable: score
#> N = 9679
#> ────────────────────────────────────────────────────────────────────
#> b S.E. t p [95% CI of b] VIF
#> ────────────────────────────────────────────────────────────────────
#> (Intercept) 51.913 (0.097) 534.035 <.001 *** [51.723, 52.104]
#> gender 1.545 (0.195) 7.938 <.001 *** [ 1.163, 1.926] 1.000
#> late -1.169 (0.086) -13.519 <.001 *** [-1.338, -0.999] 1.001
#> gender:late -0.462 (0.173) -2.673 .008 ** [-0.800, -0.123] 1.001
#> ────────────────────────────────────────────────────────────────────
#>
#> Standardized Coefficients (β):
#> Outcome Variable: score
#> N = 9679
#> ─────────────────────────────────────────────────────────────────────────────────
#> β S.E. t p [95% CI of β] r(partial) r(part)
#> ─────────────────────────────────────────────────────────────────────────────────
#> gender 0.080 (0.010) 7.938 <.001 *** [ 0.060, 0.099] 0.080 0.080
#> late -0.136 (0.010) -13.519 <.001 *** [-0.155, -0.116] -0.136 -0.136
#> gender:late -0.027 (0.010) -2.673 .008 ** [-0.047, -0.007] -0.027 -0.027
#> ─────────────────────────────────────────────────────────────────────────────────
#>
# (allows multicategorical moderator)
d = airquality
d$Month = as.factor(d$Month) # moderator: factor with levels "5"~"9"
PROCESS(d, y="Temp", x="Solar.R", mods="Month")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 1
#> Model Type : Simple Moderation
#> - Outcome (Y) : Temp
#> - Predictor (X) : Solar.R
#> - Mediators (M) : -
#> - Moderators (W) : Month
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - Temp ~ Solar.R*Month
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ────────────────────────────────────────
#> (1) Temp (2) Temp
#> ────────────────────────────────────────
#> (Intercept) 78.116 *** 66.012 ***
#> (0.736) (1.232)
#> Solar.R 0.028 *** 0.027 *
#> (0.008) (0.011)
#> Month6 12.967 ***
#> (1.699)
#> Month7 17.366 ***
#> (1.742)
#> Month8 18.235 ***
#> (1.741)
#> Month9 11.129 ***
#> (1.721)
#> Solar.R:Month6 0.002
#> (0.017)
#> Solar.R:Month7 -0.009
#> (0.018)
#> Solar.R:Month8 0.009
#> (0.019)
#> Solar.R:Month9 -0.014
#> (0.019)
#> ────────────────────────────────────────
#> R^2 0.076 0.549
#> Adj. R^2 0.070 0.519
#> Num. obs. 146 146
#> ────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Simple Moderation (Model 1)
#> Sample Size : 146 (7 missing observations deleted)
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effect on "Temp" (Y)
#> ───────────────────────────────────────
#> F df1 df2 p
#> ───────────────────────────────────────
#> Solar.R * Month 0.36 4 136 .838
#> ───────────────────────────────────────
#>
#> Simple Slopes: "Solar.R" (X) ==> "Temp" (Y)
#> ───────────────────────────────────────────────────────
#> "Month" Effect S.E. t p [95% CI]
#> ───────────────────────────────────────────────────────
#> 5 0.027 (0.011) 2.432 .016 * [ 0.005, 0.048]
#> 6 0.029 (0.013) 2.242 .027 * [ 0.003, 0.054]
#> 7 0.017 (0.014) 1.186 .238 [-0.011, 0.046]
#> 8 0.035 (0.016) 2.202 .029 * [ 0.004, 0.067]
#> 9 0.013 (0.015) 0.865 .389 [-0.017, 0.043]
#> ───────────────────────────────────────────────────────
#>
## Model 2 ##
PROCESS(data, y="score", x="late",
mods=c("gender", "family_inc"),
mod.type="2-way") # or omit "mod.type", default is "2-way"
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 2
#> Model Type : Parallel Moderation (2 mods; 2-way)
#> - Outcome (Y) : score
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender, family_inc
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ late*gender + late*family_inc
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ───────────────────────────────────────────
#> (1) score (2) score
#> ───────────────────────────────────────────
#> (Intercept) 51.912 *** 51.255 ***
#> (0.098) (0.127)
#> late -1.174 *** -0.836 ***
#> (0.087) (0.115)
#> genderMale 1.375 ***
#> (0.184)
#> family_inc 1.339 ***
#> (0.040)
#> late:genderMale -0.301
#> (0.163)
#> late:family_inc 0.007
#> (0.034)
#> ───────────────────────────────────────────
#> R^2 0.019 0.129
#> Adj. R^2 0.018 0.129
#> Num. obs. 9679 9679
#> ───────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Parallel Moderation (2 mods; 2-way) (Model 2)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effects on "score" (Y)
#> ───────────────────────────────────────────
#> F df1 df2 p
#> ───────────────────────────────────────────
#> late * gender 3.40 1 9673 .065 .
#> late * family_inc 0.04 1 9673 .849
#> (All Interactions) 1.72 2 9673 .179
#> ───────────────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "score" (Y)
#> ────────────────────────────────────────────────────────────────────────
#> "family_inc" "gender" Effect S.E. t p [95% CI]
#> ────────────────────────────────────────────────────────────────────────
#> 6.923 (- SD) Female -0.851 (0.137) -6.219 <.001 *** [-1.119, -0.583]
#> 6.923 (- SD) Male -1.152 (0.138) -8.369 <.001 *** [-1.422, -0.882]
#> 9.258 (Mean) Female -0.836 (0.115) -7.238 <.001 *** [-1.062, -0.609]
#> 9.258 (Mean) Male -1.137 (0.116) -9.792 <.001 *** [-1.365, -0.909]
#> 11.594 (+ SD) Female -0.820 (0.144) -5.699 <.001 *** [-1.103, -0.538]
#> 11.594 (+ SD) Male -1.122 (0.144) -7.778 <.001 *** [-1.405, -0.839]
#> ────────────────────────────────────────────────────────────────────────
#>
## Model 3 ##
PROCESS(data, y="score", x="late",
mods=c("gender", "family_inc"),
mod.type="3-way")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 3
#> Model Type : Moderated Moderation (2 mods; 3-way)
#> - Outcome (Y) : score
#> - Predictor (X) : late
#> - Mediators (M) : -
#> - Moderators (W) : gender, family_inc
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - score ~ late*gender*family_inc
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ──────────────────────────────────────────────────────
#> (1) score (2) score
#> ──────────────────────────────────────────────────────
#> (Intercept) 51.912 *** 51.266 ***
#> (0.098) (0.127)
#> late -1.174 *** -0.818 ***
#> (0.087) (0.116)
#> genderMale 1.348 ***
#> (0.185)
#> family_inc 1.375 ***
#> (0.055)
#> late:genderMale -0.339 *
#> (0.164)
#> late:family_inc 0.088
#> (0.050)
#> genderMale:family_inc -0.069
#> (0.079)
#> late:genderMale:family_inc -0.153 *
#> (0.069)
#> ──────────────────────────────────────────────────────
#> R^2 0.019 0.130
#> Adj. R^2 0.018 0.129
#> Num. obs. 9679 9679
#> ──────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Moderated Moderation (2 mods; 3-way) (Model 3)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effects on "score" (Y)
#> ───────────────────────────────────────────────────
#> F df1 df2 p
#> ───────────────────────────────────────────────────
#> late * gender 4.26 1 9671 .039 *
#> late * family_inc 3.11 1 9671 .078 .
#> gender * family_inc 0.75 1 9671 .386
#> late * gender * family_inc 4.95 1 9671 .026 *
#> (All Interactions) 2.33 4 9671 .054 .
#> ───────────────────────────────────────────────────
#>
#> Conditional Interaction Effects on "score" (Y)
#> ────────────────────────────────────────────────────
#> "family_inc" Interaction F df1 df2 p
#> ────────────────────────────────────────────────────
#> 6.923 (- SD) late * gender 0.01 1 9671 .938
#> 9.258 (Mean) late * gender 4.26 1 9671 .039 *
#> 11.594 (+ SD) late * gender 8.56 1 9671 .003 **
#> ────────────────────────────────────────────────────
#>
#> Simple Slopes: "late" (X) ==> "score" (Y)
#> ────────────────────────────────────────────────────────────────────────
#> "family_inc" "gender" Effect S.E. t p [95% CI]
#> ────────────────────────────────────────────────────────────────────────
#> 6.923 (- SD) Female -1.022 (0.157) -6.506 <.001 *** [-1.330, -0.714]
#> 6.923 (- SD) Male -1.005 (0.155) -6.470 <.001 *** [-1.309, -0.700]
#> 9.258 (Mean) Female -0.818 (0.116) -7.068 <.001 *** [-1.044, -0.591]
#> 9.258 (Mean) Male -1.157 (0.117) -9.927 <.001 *** [-1.385, -0.928]
#> 11.594 (+ SD) Female -0.613 (0.170) -3.604 <.001 *** [-0.947, -0.280]
#> 11.594 (+ SD) Male -1.308 (0.166) -7.894 <.001 *** [-1.633, -0.983]
#> ────────────────────────────────────────────────────────────────────────
#>
PROCESS(data, y="pass", x="gender",
mods=c("late", "family_inc"),
mod1.val=c(1, 3, 5), # moderator 1: late
mod2.val=seq(1, 15, 2), # moderator 2: family_inc
mod.type="3-way")
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 3
#> Model Type : Moderated Moderation (2 mods; 3-way)
#> - Outcome (Y) : pass
#> - Predictor (X) : gender (recoded: Female=0, Male=1)
#> - Mediators (M) : -
#> - Moderators (W) : late, family_inc
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Outcome:
#> - pass ~ gender*late*family_inc
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ────────────────────────────────────────────────────
#> (1) pass (2) pass
#> ────────────────────────────────────────────────────
#> (Intercept) 0.414 *** 0.442 ***
#> (0.021) (0.022)
#> gender 0.228 *** 0.219 ***
#> (0.042) (0.044)
#> late -0.216 ***
#> (0.019)
#> family_inc 0.259 ***
#> (0.010)
#> gender:late -0.046
#> (0.039)
#> gender:family_inc -0.022
#> (0.020)
#> late:family_inc 0.005
#> (0.009)
#> gender:late:family_inc -0.032
#> (0.018)
#> ────────────────────────────────────────────────────
#> McFadden's R^2 0.002 0.073
#> Nagelkerke's R^2 0.004 0.127
#> AIC 12989.483 12080.387
#> BIC 13003.839 12137.809
#> Num. obs. 9679 9679
#> ────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘interactions’ (v1.2.0)
#> Effect Type : Moderated Moderation (2 mods; 3-way) (Model 3)
#> Sample Size : 9679
#> Random Seed : -
#> Simulations : -
#>
#> Interaction Effects on "pass" (Y)
#> ──────────────────────────────────────────────
#> Chisq df p
#> ──────────────────────────────────────────────
#> gender * late 1.43 1 .231
#> gender * family_inc 1.17 1 .279
#> late * family_inc 0.32 1 .573
#> gender * late * family_inc 3.18 1 .075 .
#> (All Interactions) 5.72 4 .221
#> ──────────────────────────────────────────────
#>
#> Conditional Interaction Effects on "pass" (Y)
#> ──────────────────────────────────────────────
#> "family_inc" Interaction Chisq df p
#> ──────────────────────────────────────────────
#> 1.000 gender * late 2.08 1 .149
#> 3.000 gender * late 1.73 1 .188
#> 5.000 gender * late 1.15 1 .285
#> 7.000 gender * late 0.22 1 .642
#> 9.000 gender * late 0.97 1 .323
#> 11.000 gender * late 3.93 1 .047 *
#> 13.000 gender * late 4.34 1 .037 *
#> 15.000 gender * late 4.19 1 .041 *
#> ──────────────────────────────────────────────
#>
#> Simple Slopes: "gender" (X) ==> "pass" (Y)
#> ────────────────────────────────────────────────────────────────────
#> "family_inc" "late" Effect S.E. z p [95% CI]
#> ────────────────────────────────────────────────────────────────────
#> 1.000 1.000 0.131 (0.253) 0.518 .605 [-0.365, 0.627]
#> 1.000 3.000 0.561 (0.201) 2.795 .005 ** [ 0.168, 0.954]
#> 1.000 5.000 0.991 (0.441) 2.247 .025 * [ 0.127, 1.855]
#> 3.000 1.000 0.166 (0.196) 0.850 .395 [-0.217, 0.550]
#> 3.000 3.000 0.470 (0.155) 3.029 .002 ** [ 0.166, 0.774]
#> 3.000 5.000 0.773 (0.341) 2.270 .023 * [ 0.106, 1.440]
#> 5.000 1.000 0.202 (0.141) 1.435 .151 [-0.074, 0.477]
#> 5.000 3.000 0.378 (0.111) 3.402 <.001 *** [ 0.160, 0.596]
#> 5.000 5.000 0.555 (0.244) 2.275 .023 * [ 0.077, 1.033]
#> 7.000 1.000 0.237 (0.092) 2.576 .010 ** [ 0.057, 0.418]
#> 7.000 3.000 0.287 (0.072) 3.962 <.001 *** [ 0.145, 0.429]
#> 7.000 5.000 0.337 (0.159) 2.124 .034 * [ 0.026, 0.649]
#> 9.000 1.000 0.272 (0.066) 4.109 <.001 *** [ 0.143, 0.402]
#> 9.000 3.000 0.196 (0.052) 3.775 <.001 *** [ 0.094, 0.298]
#> 9.000 5.000 0.120 (0.114) 1.049 .294 [-0.104, 0.343]
#> 11.000 1.000 0.308 (0.087) 3.544 <.001 *** [ 0.138, 0.478]
#> 11.000 3.000 0.105 (0.069) 1.529 .126 [-0.030, 0.239]
#> 11.000 5.000 -0.098 (0.151) -0.650 .515 [-0.395, 0.198]
#> 13.000 1.000 0.343 (0.134) 2.564 .010 * [ 0.081, 0.606]
#> 13.000 3.000 0.014 (0.106) 0.128 .898 [-0.194, 0.221]
#> 13.000 5.000 -0.316 (0.234) -1.351 .177 [-0.775, 0.143]
#> 15.000 1.000 0.379 (0.188) 2.009 .045 * [ 0.009, 0.748]
#> 15.000 3.000 -0.078 (0.150) -0.520 .603 [-0.371, 0.215]
#> 15.000 5.000 -0.534 (0.330) -1.619 .105 [-1.181, 0.113]
#> ────────────────────────────────────────────────────────────────────
#>
## Model 4 ##
PROCESS(data, y="score", x="parent_edu",
meds="family_inc", covs="gender",
ci="boot", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 4
#> Model Type : Simple Mediation
#> - Outcome (Y) : score
#> - Predictor (X) : parent_edu
#> - Mediators (M) : family_inc
#> - Moderators (W) : -
#> - Covariates (C) : gender
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - family_inc ~ gender + parent_edu
#> Formula of Outcome:
#> - score ~ gender + parent_edu + family_inc
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ───────────────────────────────────────────────────────
#> (1) score (2) family_inc (3) score
#> ───────────────────────────────────────────────────────
#> (Intercept) 51.206 *** 9.207 *** 51.262 ***
#> (0.130) (0.030) (0.126)
#> genderMale 1.474 *** 0.108 * 1.358 ***
#> (0.188) (0.044) (0.182)
#> parent_edu 5.537 *** 1.793 *** 3.594 ***
#> (0.190) (0.044) (0.199)
#> family_inc 1.083 ***
#> (0.042)
#> ───────────────────────────────────────────────────────
#> R^2 0.087 0.146 0.145
#> Adj. R^2 0.086 0.146 0.145
#> Num. obs. 9679 9679 9679
#> ───────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘mediation’ (v4.5.1)
#> Effect Type : Simple Mediation (Model 4)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Bootstrap)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Running 100 simulations...
#> Indirect Path: "parent_edu" (X) ==> "family_inc" (M) ==> "score" (Y)
#> ─────────────────────────────────────────────────────────────
#> Effect S.E. z p [Boot 95% CI]
#> ─────────────────────────────────────────────────────────────
#> Indirect (ab) 1.943 (0.089) 21.759 <.001 *** [1.752, 2.095]
#> Direct (c') 3.594 (0.220) 16.319 <.001 *** [3.155, 3.981]
#> Total (c) 5.537 (0.203) 27.249 <.001 *** [5.084, 5.898]
#> ─────────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
# (allows an infinite number of multiple mediators in parallel)
PROCESS(data, y="score", x="parent_edu",
meds=c("family_inc", "late"),
covs=c("gender", "partjob"),
ci="boot", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 4
#> Model Type : Parallel Multiple Mediation (2 meds)
#> - Outcome (Y) : score
#> - Predictor (X) : parent_edu
#> - Mediators (M) : family_inc, late
#> - Moderators (W) : -
#> - Covariates (C) : gender, partjob
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - family_inc ~ gender + partjob + parent_edu
#> - late ~ gender + partjob + parent_edu
#> Formula of Outcome:
#> - score ~ gender + partjob + parent_edu + family_inc + late
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ─────────────────────────────────────────────────────────────────────
#> (1) score (2) family_inc (3) late (4) score
#> ─────────────────────────────────────────────────────────────────────
#> (Intercept) 51.206 *** 9.207 *** 2.235 *** 51.254 ***
#> (0.130) (0.030) (0.016) (0.125)
#> genderMale 1.475 *** 0.107 * 0.013 1.374 ***
#> (0.188) (0.044) (0.023) (0.181)
#> partjob -0.301 0.132 ** 0.091 *** -0.353
#> (0.193) (0.045) (0.023) (0.186)
#> parent_edu 5.531 *** 1.796 *** -0.092 *** 3.545 ***
#> (0.190) (0.044) (0.023) (0.197)
#> family_inc 1.057 ***
#> (0.042)
#> late -0.957 ***
#> (0.081)
#> ─────────────────────────────────────────────────────────────────────
#> R^2 0.087 0.146 0.003 0.158
#> Adj. R^2 0.087 0.146 0.003 0.157
#> Num. obs. 9679 9679 9679 9679
#> ─────────────────────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘mediation’ (v4.5.1)
#> Effect Type : Parallel Multiple Mediation (2 meds) (Model 4)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Bootstrap)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Running 100 simulations...
#> Indirect Path: "parent_edu" (X) ==> "family_inc" (M) ==> "score" (Y)
#> ─────────────────────────────────────────────────────────────
#> Effect S.E. z p [Boot 95% CI]
#> ─────────────────────────────────────────────────────────────
#> Indirect (ab) 1.898 (0.089) 21.262 <.001 *** [1.711, 2.055]
#> Direct (c') 3.545 (0.218) 16.280 <.001 *** [3.089, 3.937]
#> ─────────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Running 100 simulations...
#> Indirect Path: "parent_edu" (X) ==> "late" (M) ==> "score" (Y)
#> ─────────────────────────────────────────────────────────────
#> Effect S.E. z p [Boot 95% CI]
#> ─────────────────────────────────────────────────────────────
#> Indirect (ab) 0.088 (0.022) 3.946 <.001 *** [0.054, 0.136]
#> Direct (c') 3.545 (0.218) 16.280 <.001 *** [3.089, 3.937]
#> ─────────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
# (multilevel mediation)
PROCESS(data, y="score", x="SCH_free",
meds="late", clusters="SCH_ID",
ci="mcmc", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 4
#> Model Type : Simple Mediation
#> - Outcome (Y) : score
#> - Predictor (X) : SCH_free
#> - Mediators (M) : late
#> - Moderators (W) : -
#> - Covariates (C) : -
#> - HLM Clusters : SCH_ID
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - late ~ SCH_free + (1 | SCH_ID)
#> Formula of Outcome:
#> - score ~ SCH_free + late + (1 | SCH_ID)
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ────────────────────────────────────────────────────────────────────
#> (1) score (2) late (3) score
#> ────────────────────────────────────────────────────────────────────
#> (Intercept) 51.853 *** 2.245 *** 51.858 ***
#> (0.162) (0.017) (0.159)
#> SCH_free -1.611 *** 0.049 *** -1.566 ***
#> (0.085) (0.009) (0.084)
#> late -0.902 ***
#> (0.082)
#> ────────────────────────────────────────────────────────────────────
#> Marginal R^2 0.095 0.007 0.106
#> Conditional R^2 0.201 0.073 0.208
#> AIC 69944.810 29498.368 69828.530
#> BIC 69973.521 29527.079 69864.419
#> Num. obs. 9679 9679 9679
#> Num. groups: SCH_ID 568 568 568
#> Var: SCH_ID (Intercept) 9.935 0.084 9.592
#> Var: Residual 75.201 1.176 74.339
#> ────────────────────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘mediation’ (v4.5.1)
#> Effect Type : Simple Mediation (Model 4)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Monte Carlo)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Running 100 simulations...
#> Indirect Path: "SCH_free" (X) ==> "late" (M) ==> "score" (Y)
#> ────────────────────────────────────────────────────────────────
#> Effect S.E. z p [MCMC 95% CI]
#> ────────────────────────────────────────────────────────────────
#> Indirect (ab) -0.044 (0.009) -5.155 <.001 *** [-0.061, -0.030]
#> Direct (c') -1.573 (0.078) -20.230 <.001 *** [-1.720, -1.440]
#> Total (c) -1.618 (0.078) -20.624 <.001 *** [-1.769, -1.480]
#> ────────────────────────────────────────────────────────────────
#> Monte Carlo (Quasi-Bayesian) Confidence Interval
#> (Effect, SE, and CI are estimated based on 100 Monte Carlo samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
## Model 6 ##
PROCESS(data, y="score", x="parent_edu",
meds=c("family_inc", "late"),
covs=c("gender", "partjob"),
med.type="serial",
ci="boot", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 6
#> Model Type : Serial Multiple Mediation (2 meds)
#> - Outcome (Y) : score
#> - Predictor (X) : parent_edu
#> - Mediators (M) : family_inc, late
#> - Moderators (W) : -
#> - Covariates (C) : gender, partjob
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - family_inc ~ gender + partjob + parent_edu
#> - late ~ gender + partjob + parent_edu + family_inc
#> Formula of Outcome:
#> - score ~ gender + partjob + parent_edu + family_inc + late
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ─────────────────────────────────────────────────────────────────────
#> (1) score (2) family_inc (3) late (4) score
#> ─────────────────────────────────────────────────────────────────────
#> (Intercept) 51.206 *** 9.207 *** 2.516 *** 51.254 ***
#> (0.130) (0.030) (0.051) (0.125)
#> genderMale 1.475 *** 0.107 * 0.017 1.374 ***
#> (0.188) (0.044) (0.023) (0.181)
#> partjob -0.301 0.132 ** 0.096 *** -0.353
#> (0.193) (0.045) (0.023) (0.186)
#> parent_edu 5.531 *** 1.796 *** -0.037 3.545 ***
#> (0.190) (0.044) (0.025) (0.197)
#> family_inc -0.030 *** 1.057 ***
#> (0.005) (0.042)
#> late -0.957 ***
#> (0.081)
#> ─────────────────────────────────────────────────────────────────────
#> R^2 0.087 0.146 0.007 0.158
#> Adj. R^2 0.087 0.146 0.006 0.157
#> Num. obs. 9679 9679 9679 9679
#> ─────────────────────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘lavaan’ (v0.6.21)
#> Effect Type : Serial Multiple Mediation (2 meds) (Model 6)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Bootstrap)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Running 100 simulations (lavaan model)...
#> LAVAAN Syntax:
#> family_inc ~ gender + partjob + a1*parent_edu
#> late ~ gender + partjob + a2*parent_edu + d12*family_inc
#> score ~ gender + partjob + c.*parent_edu + b1*family_inc + b2*late
#> Indirect_All := a1*b1 + a2*b2 + a1*d12*b2
#> Ind_X_M1_Y := a1*b1
#> Ind_X_M2_Y := a2*b2
#> Ind_X_M1_M2_Y := a1*d12*b2
#> Direct := c.
#> Total := c. + a1*b1 + a2*b2 + a1*d12*b2
#> ────────────────────────────────────────────────────────────────────────
#> Estimate S.E. z p [Boot 95% CI] Beta
#> ────────────────────────────────────────────────────────────────────────
#> Indirect_All 1.986 (0.088) 22.644 <.001 *** [ 1.798, 2.135] 0.102
#> Ind_X_M1_Y 1.898 (0.083) 22.816 <.001 *** [ 1.724, 2.058] 0.097
#> Ind_X_M2_Y 0.036 (0.027) 1.327 .185 [-0.011, 0.086] 0.002
#> Ind_X_M1_M2_Y 0.052 (0.011) 4.774 <.001 *** [ 0.034, 0.078] 0.003
#> Direct 3.545 (0.178) 19.879 <.001 *** [ 3.179, 3.825] 0.182
#> Total 5.531 (0.171) 32.290 <.001 *** [ 5.130, 5.857] 0.283
#> ────────────────────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
## Model 8 ##
PROCESS(data, y="score", x="fight",
meds="late",
mods="gender",
mod.path=c("x-m", "x-y"),
ci="boot", nsim=100, seed=1)
#>
#> ****************** PART 1. Regression Model Summary ******************
#>
#> PROCESS Model ID : 8
#> Model Type : Moderated Mediation
#> - Outcome (Y) : score
#> - Predictor (X) : fight
#> - Mediators (M) : late
#> - Moderators (W) : gender
#> - Covariates (C) : -
#> - HLM Clusters : -
#>
#> All numeric predictors have been grand-mean centered.
#> (For details, please see the help page of PROCESS.)
#>
#> Formula of Mediator:
#> - late ~ fight*gender
#> Formula of Outcome:
#> - score ~ fight*gender + late
#>
#> CAUTION:
#> Fixed effect (coef.) of a predictor involved in an interaction
#> denotes its "simple effect/slope" at the other predictor = 0.
#> Only when all predictors in an interaction are mean-centered
#> can the fixed effect be interpreted as "main effect"!
#>
#> Model Summary
#>
#> ──────────────────────────────────────────────────────────
#> (1) score (2) late (3) score
#> ──────────────────────────────────────────────────────────
#> (Intercept) 51.912 *** 2.272 *** 50.824 ***
#> (0.097) (0.016) (0.136)
#> fight -4.585 *** 0.646 *** -6.188 ***
#> (0.293) (0.062) (0.527)
#> genderMale -0.057 * 2.129 ***
#> (0.023) (0.196)
#> fight:genderMale -0.103 2.305 ***
#> (0.074) (0.633)
#> late -0.950 ***
#> (0.087)
#> ──────────────────────────────────────────────────────────
#> R^2 0.025 0.028 0.050
#> Adj. R^2 0.025 0.028 0.049
#> Num. obs. 9679 9679 9679
#> ──────────────────────────────────────────────────────────
#> Note. * p < .05, ** p < .01, *** p < .001.
#>
#> ************ PART 2. Mediation/Moderation Effect Estimate ************
#>
#> Package Use : ‘mediation’ (v4.5.1), ‘interactions’ (v1.2.0)
#> Effect Type : Moderated Mediation (Model 8)
#> Sample Size : 9679
#> Random Seed : set.seed(1)
#> Simulations : 100 (Bootstrap)
#>
#> Warning: nsim=1000 (or larger) is suggested!
#>
#> Interaction Effect on "score" (Y)
#> ────────────────────────────────────────
#> F df1 df2 p
#> ────────────────────────────────────────
#> fight * gender 13.24 1 9674 <.001 ***
#> ────────────────────────────────────────
#>
#> Simple Slopes: "fight" (X) ==> "score" (Y)
#> (Conditional Direct Effects [c'] of X on Y)
#> ───────────────────────────────────────────────────────────
#> "gender" Effect S.E. t p [95% CI]
#> ───────────────────────────────────────────────────────────
#> Female -6.188 (0.527) -11.742 <.001 *** [-7.221, -5.155]
#> Male -3.883 (0.359) -10.821 <.001 *** [-4.587, -3.180]
#> ───────────────────────────────────────────────────────────
#>
#> Interaction Effect on "late" (M)
#> ───────────────────────────────────────
#> F df1 df2 p
#> ───────────────────────────────────────
#> fight * gender 1.90 1 9675 .168
#> ───────────────────────────────────────
#>
#> Simple Slopes: "fight" (X) ==> "late" (M)
#> (Conditional Effects [a] of X on M)
#> ────────────────────────────────────────────────────────
#> "gender" Effect S.E. t p [95% CI]
#> ────────────────────────────────────────────────────────
#> Female 0.646 (0.062) 10.485 <.001 *** [0.525, 0.766]
#> Male 0.543 (0.042) 12.989 <.001 *** [0.461, 0.625]
#> ────────────────────────────────────────────────────────
#>
#> Running 100 * 2 simulations...
#> Indirect Path: "fight" (X) ==> "late" (M) ==> "score" (Y)
#> (Conditional Indirect Effects [ab] of X through M on Y)
#> ──────────────────────────────────────────────────────────
#> "gender" Effect S.E. z p [Boot 95% CI]
#> ──────────────────────────────────────────────────────────
#> Female -0.614 (0.086) -7.117 <.001 *** [-0.807, -0.477]
#> Male -0.516 (0.060) -8.538 <.001 *** [-0.645, -0.411]
#> ──────────────────────────────────────────────────────────
#> Percentile Bootstrap Confidence Interval
#> (SE and CI are estimated based on 100 Bootstrap samples.)
#>
#> Note. The results based on bootstrapping or other random processes
#> are unlikely identical to other statistical software (e.g., SPSS).
#> To make results reproducible, you need to set a seed (any number).
#> Please see the help page for details: help(PROCESS)
#> Ignore this note if you have already set a seed. :)
#>
## For more examples and details, see:
## https://github.com/psychbruce/bruceR/tree/main/note