Skip to contents

Multi-factor ANOVA.

Source: R/bruceR-stats_3_manova.R
MANOVA.Rd

Multi-factor ANOVA (between-subjects, within-subjects, and mixed designs), with and without covariates (ANCOVA). This function is based on and extends afex::aov_ez(). You only need to specify the data, dependent variable(s), and factors (between-subjects and/or within-subjects). Almost all results you need will be displayed together, including effect sizes (partial \(\eta^2\)) and their confidence intervals (CIs). 90% CIs for partial \(\eta^2\) (two-sided) are reported, following Steiger (2004). In addition, it reports generalized \(\eta^2\), following Olejnik & Algina (2003).

Usage

MANOVA(
  data,
  subID = NULL,
  dv = NULL,
  dvs = NULL,
  dvs.pattern = NULL,
  between = NULL,
  within = NULL,
  covariate = NULL,
  ss.type = "III",
  sph.correction = "none",
  aov.include = FALSE,
  digits = 3,
  file = NULL
)

Arguments

data

Data frame. Both wide-format and long-format are supported.

subID

Subject ID (the column name). Only necessary for long-format data.

dv

Dependent variable.

  • For wide-format data, dv only can be used for between-subjects designs. For within-subjects and mixed designs, please use dvs and dvs.pattern.

  • For long-format data, dv is the outcome variable.

dvs

Repeated measures. Only for wide-format data (within-subjects or mixed designs).

Can be:

  • "start:stop" to specify the range of variables (sensitive to the order of variables):

    e.g., "A1B1:A2B3" is matched to all variables in the data between "A1B1" and "A2B3"

  • a character vector to directly specify variables (insensitive to the order of variables):

    e.g., c("Cond1", "Cond2", "Cond3") or cc("Cond1, Cond2, Cond3")

    See cc() for its usage.

dvs.pattern

If you use dvs, you should also specify the pattern of variable names using regular expression.

Examples:

  • "Cond(.)" extracts levels from "Cond1", "Cond2", "Cond3", ... You may rename the factor using the within argument (e.g., within="Condition")

  • "X(..)Y(..)" extracts levels from "X01Y01", "X02Y02", "XaaYbc", ...

  • "X(.+)Y(.+)" extracts levels from "X1Y1", "XaYb", "XaY002", ...

Tips on regular expression:

  • "(.)" extracts any single character (number, letter, and other symbols)

  • "(.+)" extracts >= 1 character(s)

  • "(.*)" extracts >= 0 character(s)

  • "([0-9])" extracts any single number

  • "([a-z])" extracts any single letter

between

Between-subjects factor(s). Multiple variables should be included in a character vector c().

within

Within-subjects factor(s). Multiple variables should be included in a character vector c().

covariate

Covariates. Multiple variables should be included in a character vector c().

ss.type

Type of sums of squares (SS) for ANOVA. Defaults to "III".

Options: "II", "III", 2, and 3.

sph.correction

[Only for repeated measures with >= 3 levels]

Sphericity correction method for adjusting the degrees of freedom (df) when the sphericity assumption is violated. Defaults to "none". If Mauchly's test of sphericity is significant, you may set it to "GG" (Greenhouse-Geisser) or "HF" (Huynh-Feldt).

aov.include

Include the aov object in the returned object? Defaults to FALSE, as suggested by afex::aov_ez() (please see the include_aov argument in this help page, which provides a detailed explanation). If TRUE, you should also specify model.type="univariate" in EMMEANS().

digits

Number of decimal places of output. Defaults to 3.

file

File name of MS Word (".doc").

Value

A result object (list) returned by afex::aov_ez() with several other elements: between, within, data.wide, data.long.

Data Preparation

How to prepare your data and specify the arguments of MANOVA()?

  • Wide-format data (one person in one row, and repeated measures in multiple columns):

    Betweem-subjects design

    MANOVA(data=, dv=, between=, ...)

    Within-subjects design

    MANOVA(data=, dvs=, dvs.pattern=, within=, ...)

    Mixed design

    MANOVA(data=, dvs=, dvs.pattern=, between=, within=, ...)

  • Long-format data (one person in multiple rows, and repeated measures in one column):

    Betweem-subjects design

    (not applicable)

    Within-subjects design

    MANOVA(data=, subID=, dv=, within=, ...)

    Mixed design

    MANOVA(data=, subID=, dv=, between=, within=, ...)

Averaging Across Multiple Observations

If observations are not uniquely identified in user-defined long-format data, the function takes averages across those multiple observations for each case. In technical details, it specifies fun_aggregate=mean in afex::aov_ez() and values_fn=mean in tidyr::pivot_wider().

Interaction Plot

You can save the returned object and use emmeans::emmip() to create an interaction plot (based on the fitted model and a formula specification). It returns a ggplot object, which can be easily modified and saved using ggplot2 syntax.

References

Olejnik, S., & Algina, J. (2003). Generalized eta and omega squared statistics: Measures of effect size for some common research designs. Psychological Methods, 8(4), 434–447.

Steiger, J. H. (2004). Beyond the F test: Effect size confidence intervals and tests of close fit in the analysis of variance and contrast analysis. Psychological Methods, 9(2), 164–182.

See also

TTEST()

EMMEANS()

bruceR-demodata

Examples

#### Between-Subjects Design ####
# \donttest{
between.1
#>    A SCORE
#> 1  1     3
#> 2  1     6
#> 3  1     4
#> 4  1     3
#> 5  1     5
#> 6  1     7
#> 7  1     5
#> 8  1     2
#> 9  2     4
#> 10 2     6
#> 11 2     4
#> 12 2     2
#> 13 2     4
#> 14 2     5
#> 15 2     3
#> 16 2     3
#> 17 3     8
#> 18 3     9
#> 19 3     8
#> 20 3     7
#> 21 3     5
#> 22 3     6
#> 23 3     7
#> 24 3     6
#> 25 4     9
#> 26 4     8
#> 27 4     8
#> 28 4     7
#> 29 4    12
#> 30 4    13
#> 31 4    12
#> 32 4    11
MANOVA(between.1, dv="SCORE", between="A")
#> 
#> ====== ANOVA (Between-Subjects Design) ======
#> 
#> Descriptives:
#> ─────────────────────
#>  "A"   Mean    S.D. n
#> ─────────────────────
#>   A1  4.375 (1.685) 8
#>   A2  3.875 (1.246) 8
#>   A3  7.000 (1.309) 8
#>   A4 10.000 (2.268) 8
#> ─────────────────────
#> Total sample size: N = 32
#> 
#> ANOVA Table:
#> Dependent variable(s):      SCORE
#> Between-subjects factor(s): A
#> Within-subjects factor(s):  –
#> Covariate(s):               –
#> ─────────────────────────────────────────────────────────────────
#>        MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ─────────────────────────────────────────────────────────────────
#> A  63.375 2.813   3  28 22.533 <.001 ***   .707 [.526, .798] .707
#> ─────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ───────────────────────────────────────
#>            Levene’s F df1 df2     p    
#> ───────────────────────────────────────
#> DV: SCORE       3.235   3  28  .037 *  
#> ───────────────────────────────────────
#> 

between.2
#>    A B SCORE
#> 1  1 1     3
#> 2  1 1     6
#> 3  1 1     4
#> 4  1 1     3
#> 5  1 2     4
#> 6  1 2     6
#> 7  1 2     4
#> 8  1 2     2
#> 9  1 3     5
#> 10 1 3     7
#> 11 1 3     5
#> 12 1 3     2
#> 13 2 1     4
#> 14 2 1     5
#> 15 2 1     3
#> 16 2 1     3
#> 17 2 2     8
#> 18 2 2     9
#> 19 2 2     8
#> 20 2 2     7
#> 21 2 3    12
#> 22 2 3    13
#> 23 2 3    12
#> 24 2 3    11
MANOVA(between.2, dv="SCORE", between=c("A", "B"))
#> 
#> ====== ANOVA (Between-Subjects Design) ======
#> 
#> Descriptives:
#> ─────────────────────────
#>  "A" "B"   Mean    S.D. n
#> ─────────────────────────
#>   A1  B1  4.000 (1.414) 4
#>   A1  B2  4.000 (1.633) 4
#>   A1  B3  4.750 (2.062) 4
#>   A2  B1  3.750 (0.957) 4
#>   A2  B2  8.000 (0.816) 4
#>   A2  B3 12.000 (0.816) 4
#> ─────────────────────────
#> Total sample size: N = 24
#> 
#> ANOVA Table:
#> Dependent variable(s):      SCORE
#> Between-subjects factor(s): A, B
#> Within-subjects factor(s):  –
#> Covariate(s):               –
#> ─────────────────────────────────────────────────────────────────────
#>            MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ─────────────────────────────────────────────────────────────────────
#> A      80.667 1.861   1  18 43.343 <.001 ***   .707 [.482, .817] .707
#> B      40.542 1.861   2  18 21.784 <.001 ***   .708 [.470, .815] .708
#> A * B  28.292 1.861   2  18 15.201 <.001 ***   .628 [.347, .763] .628
#> ─────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ───────────────────────────────────────
#>            Levene’s F df1 df2     p    
#> ───────────────────────────────────────
#> DV: SCORE       0.605   5  18  .697    
#> ───────────────────────────────────────
#> 

between.3
#>    A B C SCORE
#> 1  1 1 1     3
#> 2  1 1 1     6
#> 3  1 1 1     4
#> 4  1 1 1     3
#> 5  1 1 2     5
#> 6  1 1 2     7
#> 7  1 1 2     5
#> 8  1 1 2     2
#> 9  1 2 1     4
#> 10 1 2 1     6
#> 11 1 2 1     4
#> 12 1 2 1     2
#> 13 1 2 2     4
#> 14 1 2 2     5
#> 15 1 2 2     3
#> 16 1 2 2     3
#> 17 2 1 1     8
#> 18 2 1 1     9
#> 19 2 1 1     8
#> 20 2 1 1     7
#> 21 2 1 2     5
#> 22 2 1 2     6
#> 23 2 1 2     7
#> 24 2 1 2     6
#> 25 2 2 1     9
#> 26 2 2 1     8
#> 27 2 2 1     8
#> 28 2 2 1     7
#> 29 2 2 2    12
#> 30 2 2 2    13
#> 31 2 2 2    12
#> 32 2 2 2    11
MANOVA(between.3, dv="SCORE", between=c("A", "B", "C"))
#> 
#> ====== ANOVA (Between-Subjects Design) ======
#> 
#> Descriptives:
#> ─────────────────────────────
#>  "A" "B" "C"   Mean    S.D. n
#> ─────────────────────────────
#>   A1  B1  C1  4.000 (1.414) 4
#>   A1  B1  C2  4.750 (2.062) 4
#>   A1  B2  C1  4.000 (1.633) 4
#>   A1  B2  C2  3.750 (0.957) 4
#>   A2  B1  C1  8.000 (0.816) 4
#>   A2  B1  C2  6.000 (0.816) 4
#>   A2  B2  C1  8.000 (0.816) 4
#>   A2  B2  C2 12.000 (0.816) 4
#> ─────────────────────────────
#> Total sample size: N = 32
#> 
#> ANOVA Table:
#> Dependent variable(s):      SCORE
#> Between-subjects factor(s): A, B, C
#> Within-subjects factor(s):  –
#> Covariate(s):               –
#> ──────────────────────────────────────────────────────────────────────────
#>                 MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ──────────────────────────────────────────────────────────────────────────
#> A          153.125 1.563   1  24 98.000 <.001 ***   .803 [.670, .870] .803
#> B           12.500 1.563   1  24  8.000  .009 **    .250 [.042, .466] .250
#> C            3.125 1.563   1  24  2.000  .170       .077 [.000, .283] .077
#> A * B       24.500 1.563   1  24 15.680 <.001 ***   .395 [.147, .585] .395
#> A * C        1.125 1.563   1  24  0.720  .405       .029 [.000, .206] .029
#> B * C       12.500 1.563   1  24  8.000  .009 **    .250 [.042, .466] .250
#> A * B * C   24.500 1.563   1  24 15.680 <.001 ***   .395 [.147, .585] .395
#> ──────────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ───────────────────────────────────────
#>            Levene’s F df1 df2     p    
#> ───────────────────────────────────────
#> DV: SCORE       0.668   7  24  .697    
#> ───────────────────────────────────────
#> 

## How to create an interaction plot using `emmeans::emmip()`?
## See help page for its usage: ?emmeans::emmip()
m = MANOVA(between.2, dv="SCORE", between=c("A", "B"))
#> 
#> ====== ANOVA (Between-Subjects Design) ======
#> 
#> Descriptives:
#> ─────────────────────────
#>  "A" "B"   Mean    S.D. n
#> ─────────────────────────
#>   A1  B1  4.000 (1.414) 4
#>   A1  B2  4.000 (1.633) 4
#>   A1  B3  4.750 (2.062) 4
#>   A2  B1  3.750 (0.957) 4
#>   A2  B2  8.000 (0.816) 4
#>   A2  B3 12.000 (0.816) 4
#> ─────────────────────────
#> Total sample size: N = 24
#> 
#> ANOVA Table:
#> Dependent variable(s):      SCORE
#> Between-subjects factor(s): A, B
#> Within-subjects factor(s):  –
#> Covariate(s):               –
#> ─────────────────────────────────────────────────────────────────────
#>            MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ─────────────────────────────────────────────────────────────────────
#> A      80.667 1.861   1  18 43.343 <.001 ***   .707 [.482, .817] .707
#> B      40.542 1.861   2  18 21.784 <.001 ***   .708 [.470, .815] .708
#> A * B  28.292 1.861   2  18 15.201 <.001 ***   .628 [.347, .763] .628
#> ─────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ───────────────────────────────────────
#>            Levene’s F df1 df2     p    
#> ───────────────────────────────────────
#> DV: SCORE       0.605   5  18  .697    
#> ───────────────────────────────────────
#> 
emmip(m, ~ A | B, CIs=TRUE)

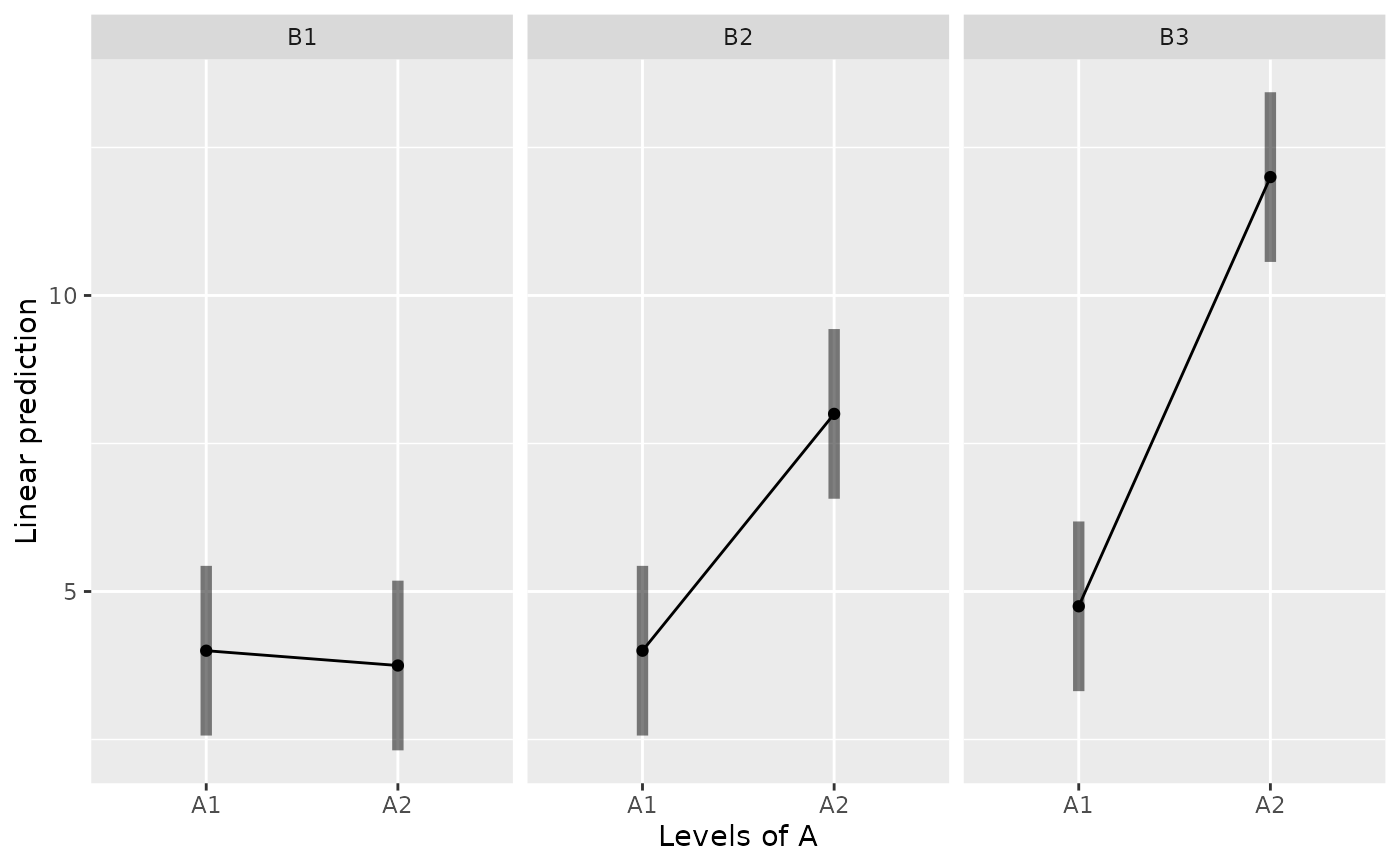emmip(m, ~ B | A, CIs=TRUE)

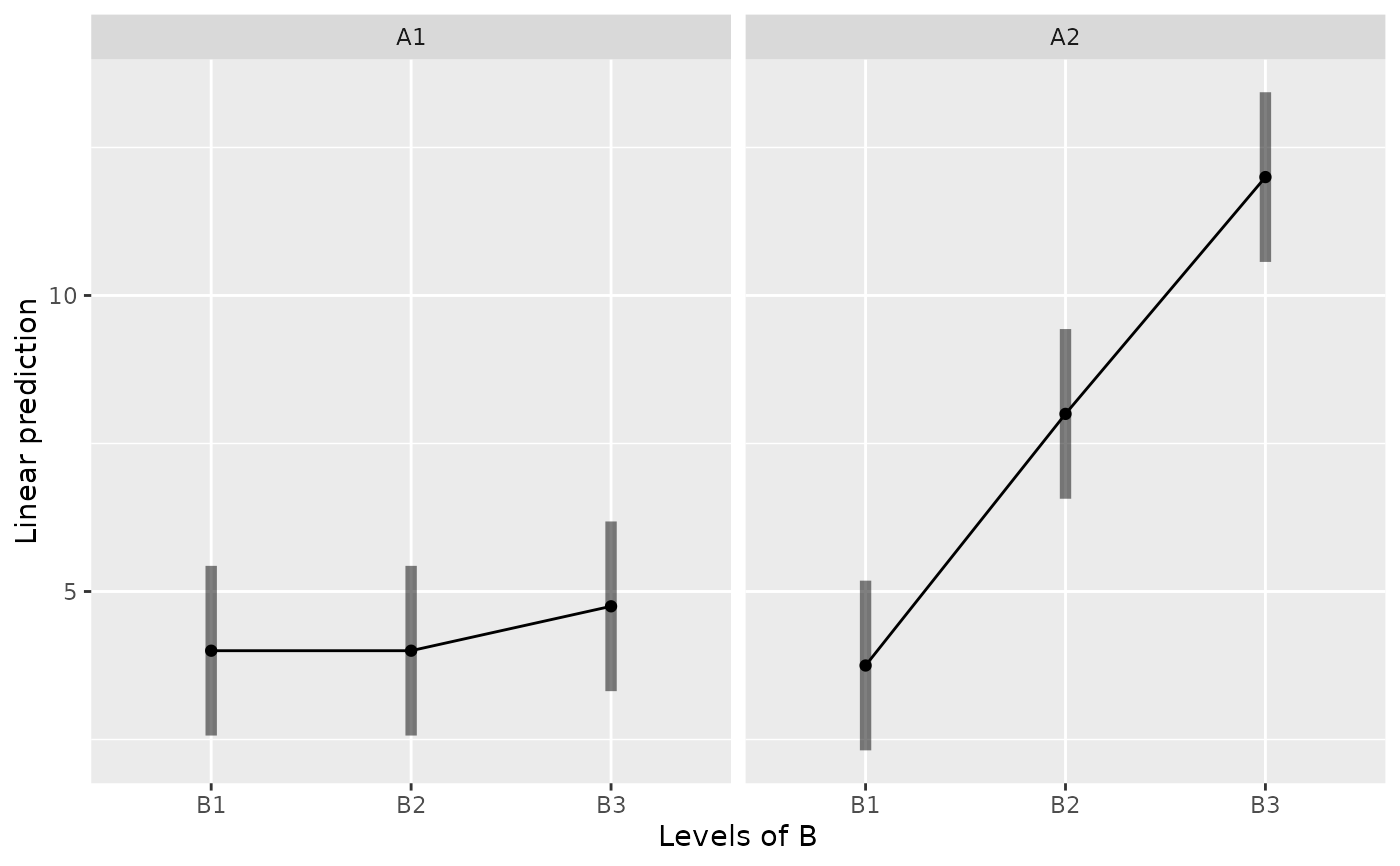emmip(m, B ~ A, CIs=TRUE)

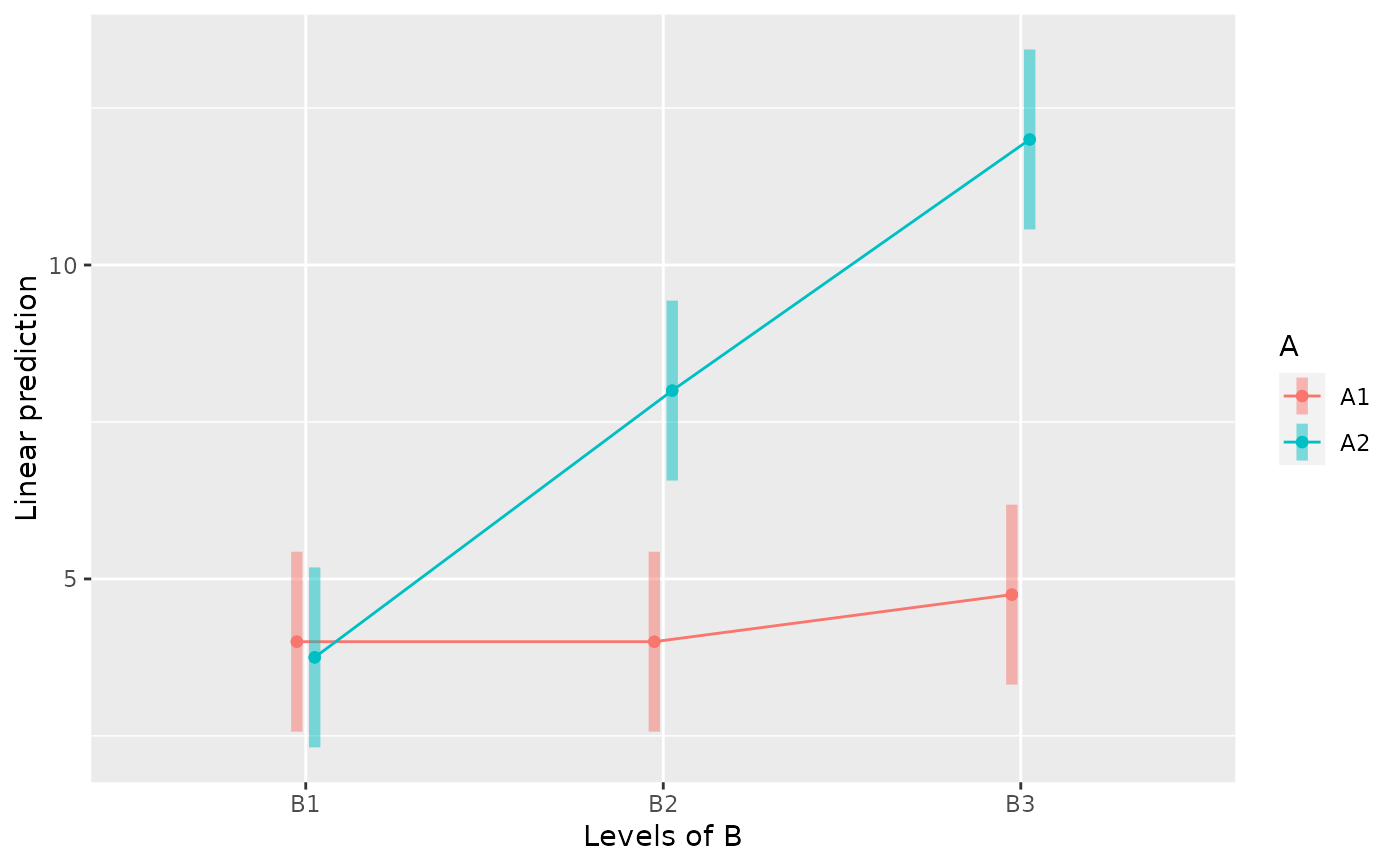
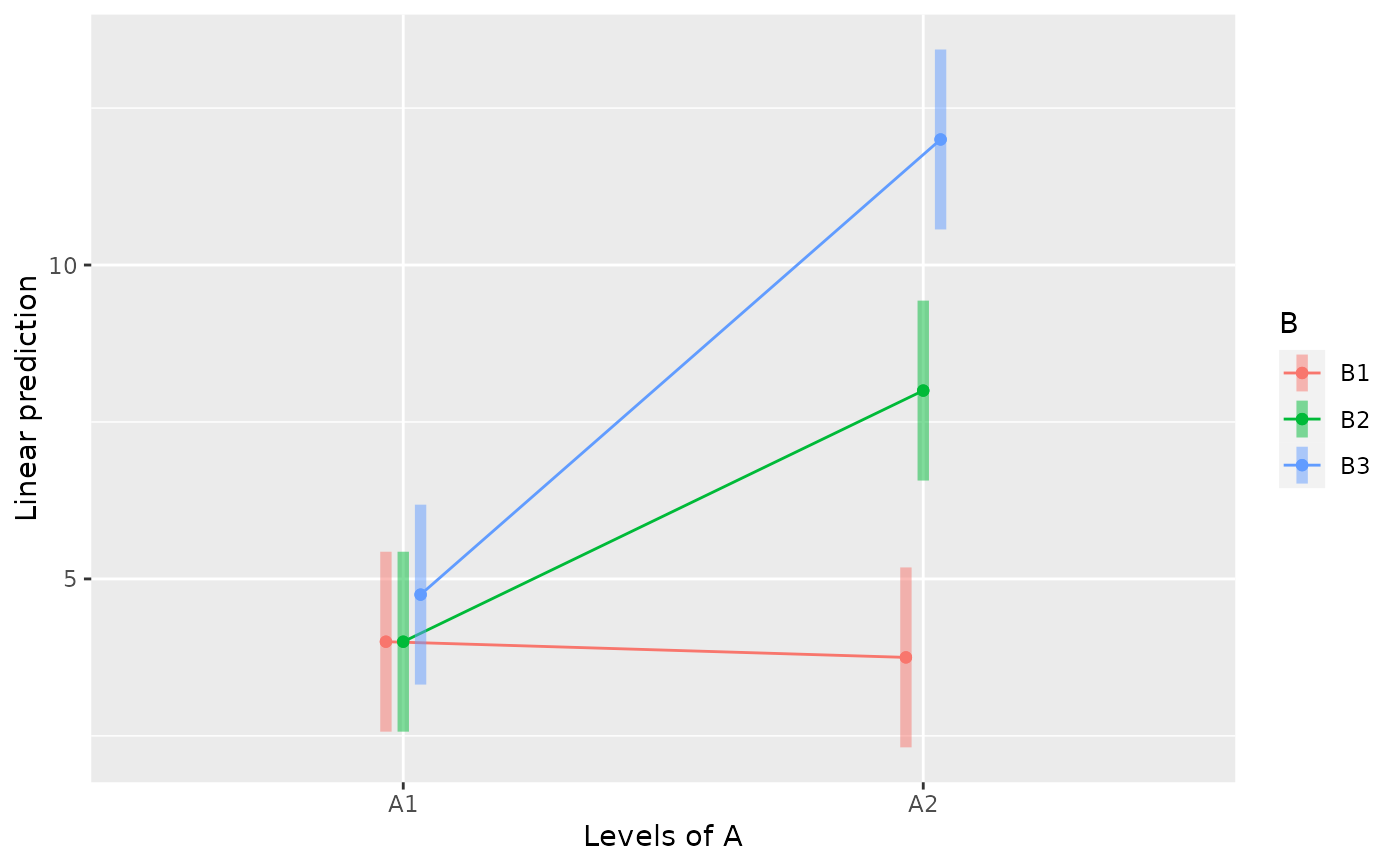emmip(m, A ~ B, CIs=TRUE)



#### Within-Subjects Design ####

within.1
#>   ID A1 A2 A3 A4
#> 1 S1  3  4  8  9
#> 2 S2  6  6  9  8
#> 3 S3  4  4  8  8
#> 4 S4  3  2  7  7
#> 5 S5  5  4  5 12
#> 6 S6  7  5  6 13
#> 7 S7  5  3  7 12
#> 8 S8  2  3  6 11
MANOVA(within.1, dvs="A1:A4", dvs.pattern="A(.)",
       within="A")
#> 
#> Note:
#> dvs="A1:A4" is matched to variables:
#> A1, A2, A3, A4
#> 
#> ====== ANOVA (Within-Subjects Design) ======
#> 
#> Descriptives:
#> ─────────────────────
#>  "A"   Mean    S.D. n
#> ─────────────────────
#>   A1  4.375 (1.685) 8
#>   A2  3.875 (1.246) 8
#>   A3  7.000 (1.309) 8
#>   A4 10.000 (2.268) 8
#> ─────────────────────
#> Total sample size: N = 8
#> 
#> ANOVA Table:
#> Dependent variable(s):      A1, A2, A3, A4
#> Between-subjects factor(s): –
#> Within-subjects factor(s):  A
#> Covariate(s):               –
#> ─────────────────────────────────────────────────────────────────
#>        MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ─────────────────────────────────────────────────────────────────
#> A  63.375 2.518   3  21 25.170 <.001 ***   .782 [.609, .858] .707
#> ─────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> No between-subjects factors. No need to do the Levene’s test.
#> 
#> Mauchly’s Test of Sphericity:
#> ────────────────────────
#>    Mauchly's W     p    
#> ────────────────────────
#> A       0.1899  .095 .  
#> ────────────────────────
#> 
## the same:
MANOVA(within.1, dvs=c("A1", "A2", "A3", "A4"), dvs.pattern="A(.)",
       within="MyFactor")  # renamed the within-subjects factor
#> 
#> ====== ANOVA (Within-Subjects Design) ======
#> 
#> Descriptives:
#> ────────────────────────────
#>  "MyFactor"   Mean    S.D. n
#> ────────────────────────────
#>   MyFactor1  4.375 (1.685) 8
#>   MyFactor2  3.875 (1.246) 8
#>   MyFactor3  7.000 (1.309) 8
#>   MyFactor4 10.000 (2.268) 8
#> ────────────────────────────
#> Total sample size: N = 8
#> 
#> ANOVA Table:
#> Dependent variable(s):      A1, A2, A3, A4
#> Between-subjects factor(s): –
#> Within-subjects factor(s):  MyFactor
#> Covariate(s):               –
#> ────────────────────────────────────────────────────────────────────────
#>               MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ────────────────────────────────────────────────────────────────────────
#> MyFactor  63.375 2.518   3  21 25.170 <.001 ***   .782 [.609, .858] .707
#> ────────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> No between-subjects factors. No need to do the Levene’s test.
#> 
#> Mauchly’s Test of Sphericity:
#> ───────────────────────────────
#>           Mauchly's W     p    
#> ───────────────────────────────
#> MyFactor       0.1899  .095 .  
#> ───────────────────────────────
#> 

within.2
#>   ID A1B1 A1B2 A1B3 A2B1 A2B2 A2B3
#> 1 S1    3    4    5    4    8   12
#> 2 S2    6    6    7    5    9   13
#> 3 S3    4    4    5    3    8   12
#> 4 S4    3    2    2    3    7   11
MANOVA(within.2, dvs="A1B1:A2B3", dvs.pattern="A(.)B(.)",
       within=c("A", "B"))
#> 
#> Note:
#> dvs="A1B1:A2B3" is matched to variables:
#> A1B1, A1B2, A1B3, A2B1, A2B2, A2B3
#> 
#> ====== ANOVA (Within-Subjects Design) ======
#> 
#> Descriptives:
#> ─────────────────────────
#>  "A" "B"   Mean    S.D. n
#> ─────────────────────────
#>   A1  B1  4.000 (1.414) 4
#>   A1  B2  4.000 (1.633) 4
#>   A1  B3  4.750 (2.062) 4
#>   A2  B1  3.750 (0.957) 4
#>   A2  B2  8.000 (0.816) 4
#>   A2  B3 12.000 (0.816) 4
#> ─────────────────────────
#> Total sample size: N = 4
#> 
#> ANOVA Table:
#> Dependent variable(s):      A1B1, A1B2, A1B3, A2B1, A2B2, A2B3
#> Between-subjects factor(s): –
#> Within-subjects factor(s):  A, B
#> Covariate(s):               –
#> ──────────────────────────────────────────────────────────────────────
#>            MS   MSE df1 df2       F     p     η²p [90% CI of η²p]  η²G
#> ──────────────────────────────────────────────────────────────────────
#> A      80.667 1.111   1   3  72.600  .003 **    .960 [.699, .985] .707
#> B      40.542 0.264   2   6 153.632 <.001 ***   .981 [.930, .991] .708
#> A * B  28.292 0.236   2   6 119.824 <.001 ***   .976 [.911, .988] .628
#> ──────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> No between-subjects factors. No need to do the Levene’s test.
#> 
#> Mauchly’s Test of Sphericity:
#> ────────────────────────────
#>        Mauchly's W     p    
#> ────────────────────────────
#> B           0.0665  .066 .  
#> A * B       0.2491  .249    
#> ────────────────────────────
#> 

within.3
#>   ID A1B1C1 A1B1C2 A1B2C1 A1B2C2 A2B1C1 A2B1C2 A2B2C1 A2B2C2
#> 1 S1      3      5      4      4      8      5      9     12
#> 2 S2      6      7      6      5      9      6      8     13
#> 3 S3      4      5      4      3      8      7      8     12
#> 4 S4      3      2      2      3      7      6      7     11
MANOVA(within.3, dvs="A1B1C1:A2B2C2", dvs.pattern="A(.)B(.)C(.)",
       within=c("A", "B", "C"))
#> 
#> Note:
#> dvs="A1B1C1:A2B2C2" is matched to variables:
#> A1B1C1, A1B1C2, A1B2C1, A1B2C2, A2B1C1, A2B1C2, A2B2C1, A2B2C2
#> 
#> ====== ANOVA (Within-Subjects Design) ======
#> 
#> Descriptives:
#> ─────────────────────────────
#>  "A" "B" "C"   Mean    S.D. n
#> ─────────────────────────────
#>   A1  B1  C1  4.000 (1.414) 4
#>   A1  B1  C2  4.750 (2.062) 4
#>   A1  B2  C1  4.000 (1.633) 4
#>   A1  B2  C2  3.750 (0.957) 4
#>   A2  B1  C1  8.000 (0.816) 4
#>   A2  B1  C2  6.000 (0.816) 4
#>   A2  B2  C1  8.000 (0.816) 4
#>   A2  B2  C2 12.000 (0.816) 4
#> ─────────────────────────────
#> Total sample size: N = 4
#> 
#> ANOVA Table:
#> Dependent variable(s):      A1B1C1, A1B1C2, A1B2C1, A1B2C2, A2B1C1, A2B1C2, A2B2C1, A2B2C2
#> Between-subjects factor(s): –
#> Within-subjects factor(s):  A, B, C
#> Covariate(s):               –
#> ──────────────────────────────────────────────────────────────────────────
#>                 MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ──────────────────────────────────────────────────────────────────────────
#> A          153.125 1.875   1   3 81.667  .003 **    .965 [.727, .986] .803
#> B           12.500 0.583   1   3 21.429  .019 *     .877 [.279, .954] .250
#> C            3.125 0.042   1   3 75.000  .003 **    .962 [.707, .985] .077
#> A * B       24.500 0.250   1   3 98.000  .002 **    .970 [.768, .989] .395
#> A * C        1.125 0.708   1   3  1.588  .297       .346 [.000, .751] .029
#> B * C       12.500 0.417   1   3 30.000  .012 *     .909 [.411, .965] .250
#> A * B * C   24.500 1.083   1   3 22.615  .018 *     .883 [.300, .956] .395
#> ──────────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> No between-subjects factors. No need to do the Levene’s test.
#> 
#> Mauchly’s Test of Sphericity:
#> The repeated measures have only two levels. The assumption of sphericity is always met.
#> 


#### Mixed Design ####

mixed.2_1b1w
#>   A B1 B2 B3
#> 1 1  3  4  5
#> 2 1  6  6  7
#> 3 1  4  4  5
#> 4 1  3  2  2
#> 5 2  4  8 12
#> 6 2  5  9 13
#> 7 2  3  8 12
#> 8 2  3  7 11
MANOVA(mixed.2_1b1w, dvs="B1:B3", dvs.pattern="B(.)",
       between="A", within="B")
#> 
#> Note:
#> dvs="B1:B3" is matched to variables:
#> B1, B2, B3
#> 
#> ====== ANOVA (Mixed Design) ======
#> 
#> Descriptives:
#> ─────────────────────────
#>  "A" "B"   Mean    S.D. n
#> ─────────────────────────
#>   A1  B1  4.000 (1.414) 4
#>   A1  B2  4.000 (1.633) 4
#>   A1  B3  4.750 (2.062) 4
#>   A2  B1  3.750 (0.957) 4
#>   A2  B2  8.000 (0.816) 4
#>   A2  B3 12.000 (0.816) 4
#> ─────────────────────────
#> Total sample size: N = 8
#> 
#> ANOVA Table:
#> Dependent variable(s):      B1, B2, B3
#> Between-subjects factor(s): A
#> Within-subjects factor(s):  B
#> Covariate(s):               –
#> ──────────────────────────────────────────────────────────────────────
#>            MS   MSE df1 df2       F     p     η²p [90% CI of η²p]  η²G
#> ──────────────────────────────────────────────────────────────────────
#> A      80.667 5.083   1   6  15.869  .007 **    .726 [.248, .871] .707
#> B      40.542 0.250   2  12 162.167 <.001 ***   .964 [.918, .980] .708
#> A * B  28.292 0.250   2  12 113.167 <.001 ***   .950 [.885, .971] .628
#> ──────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ────────────────────────────────────
#>         Levene’s F df1 df2     p    
#> ────────────────────────────────────
#> DV: B1       0.300   1   6  .604    
#> DV: B2       0.600   1   6  .468    
#> DV: B3       1.485   1   6  .269    
#> ────────────────────────────────────
#> 
#> Mauchly’s Test of Sphericity:
#> ────────────────────────────
#>        Mauchly's W     p    
#> ────────────────────────────
#> B           0.1574  .010 ** 
#> A * B       0.1574  .010 ** 
#> ────────────────────────────
#> The sphericity assumption is violated.
#> You may specify: sph.correction="GG" (or ="HF")
#> 
MANOVA(mixed.2_1b1w, dvs="B1:B3", dvs.pattern="B(.)",
       between="A", within="B", sph.correction="GG")
#> 
#> Note:
#> dvs="B1:B3" is matched to variables:
#> B1, B2, B3
#> 
#> ====== ANOVA (Mixed Design) ======
#> 
#> Descriptives:
#> ─────────────────────────
#>  "A" "B"   Mean    S.D. n
#> ─────────────────────────
#>   A1  B1  4.000 (1.414) 4
#>   A1  B2  4.000 (1.633) 4
#>   A1  B3  4.750 (2.062) 4
#>   A2  B1  3.750 (0.957) 4
#>   A2  B2  8.000 (0.816) 4
#>   A2  B3 12.000 (0.816) 4
#> ─────────────────────────
#> Total sample size: N = 8
#> 
#> ANOVA Table:
#> Dependent variable(s):      B1, B2, B3
#> Between-subjects factor(s): A
#> Within-subjects factor(s):  B
#> Covariate(s):               –
#> ──────────────────────────────────────────────────────────────────────────
#>            MS   MSE   df1   df2       F     p     η²p [90% CI of η²p]  η²G
#> ──────────────────────────────────────────────────────────────────────────
#> A      80.667 5.083 1.000 6.000  15.869  .007 **    .726 [.248, .871] .707
#> B      74.702 0.461 1.085 6.513 162.167 <.001 ***   .964 [.880, .983] .708
#> A * B  52.130 0.461 1.085 6.513 113.167 <.001 ***   .950 [.833, .976] .628
#> ──────────────────────────────────────────────────────────────────────────
#> Sphericity correction method: GG (Greenhouse-Geisser)
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ────────────────────────────────────
#>         Levene’s F df1 df2     p    
#> ────────────────────────────────────
#> DV: B1       0.300   1   6  .604    
#> DV: B2       0.600   1   6  .468    
#> DV: B3       1.485   1   6  .269    
#> ────────────────────────────────────
#> 
#> Mauchly’s Test of Sphericity:
#> ────────────────────────────
#>        Mauchly's W     p    
#> ────────────────────────────
#> B           0.1574  .010 ** 
#> A * B       0.1574  .010 ** 
#> ────────────────────────────
#> 

mixed.3_1b2w
#>   A B1C1 B1C2 B2C1 B2C2
#> 1 1    3    5    4    4
#> 2 1    6    7    6    5
#> 3 1    4    5    4    3
#> 4 1    3    2    2    3
#> 5 2    8    5    9   12
#> 6 2    9    6    8   13
#> 7 2    8    7    8   12
#> 8 2    7    6    7   11
MANOVA(mixed.3_1b2w, dvs="B1C1:B2C2", dvs.pattern="B(.)C(.)",
       between="A", within=c("B", "C"))
#> 
#> Note:
#> dvs="B1C1:B2C2" is matched to variables:
#> B1C1, B1C2, B2C1, B2C2
#> 
#> ====== ANOVA (Mixed Design) ======
#> 
#> Descriptives:
#> ─────────────────────────────
#>  "A" "B" "C"   Mean    S.D. n
#> ─────────────────────────────
#>   A1  B1  C1  4.000 (1.414) 4
#>   A1  B1  C2  4.750 (2.062) 4
#>   A1  B2  C1  4.000 (1.633) 4
#>   A1  B2  C2  3.750 (0.957) 4
#>   A2  B1  C1  8.000 (0.816) 4
#>   A2  B1  C2  6.000 (0.816) 4
#>   A2  B2  C1  8.000 (0.816) 4
#>   A2  B2  C2 12.000 (0.816) 4
#> ─────────────────────────────
#> Total sample size: N = 8
#> 
#> ANOVA Table:
#> Dependent variable(s):      B1C1, B1C2, B2C1, B2C2
#> Between-subjects factor(s): A
#> Within-subjects factor(s):  B, C
#> Covariate(s):               –
#> ──────────────────────────────────────────────────────────────────────────
#>                 MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ──────────────────────────────────────────────────────────────────────────
#> A          153.125 4.708   1   6 32.522  .001 **    .844 [.503, .926] .803
#> B           12.500 0.417   1   6 30.000  .002 **    .833 [.475, .921] .250
#> A * B       24.500 0.417   1   6 58.800 <.001 ***   .907 [.684, .956] .395
#> C            3.125 0.375   1   6  8.333  .028 *     .581 [.064, .801] .077
#> A * C        1.125 0.375   1   6  3.000  .134       .333 [.000, .671] .029
#> B * C       12.500 0.750   1   6 16.667  .006 **    .735 [.264, .875] .250
#> A * B * C   24.500 0.750   1   6 32.667  .001 **    .845 [.505, .927] .395
#> ──────────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ──────────────────────────────────────
#>           Levene’s F df1 df2     p    
#> ──────────────────────────────────────
#> DV: B1C1       1.000   1   6  .356    
#> DV: B1C2       1.485   1   6  .269    
#> DV: B2C1       0.600   1   6  .468    
#> DV: B2C2       0.500   1   6  .506    
#> ──────────────────────────────────────
#> 
#> Mauchly’s Test of Sphericity:
#> The repeated measures have only two levels. The assumption of sphericity is always met.
#> 

mixed.3_2b1w
#>    A C B1 B2
#> 1  1 1  3  4
#> 2  1 1  6  6
#> 3  1 1  4  4
#> 4  1 1  3  2
#> 5  1 2  5  4
#> 6  1 2  7  5
#> 7  1 2  5  3
#> 8  1 2  2  3
#> 9  2 1  8  9
#> 10 2 1  9  8
#> 11 2 1  8  8
#> 12 2 1  7  7
#> 13 2 2  5 12
#> 14 2 2  6 13
#> 15 2 2  7 12
#> 16 2 2  6 11
MANOVA(mixed.3_2b1w, dvs="B1:B2", dvs.pattern="B(.)",
       between=c("A", "C"), within="B")
#> 
#> Note:
#> dvs="B1:B2" is matched to variables:
#> B1, B2
#> 
#> ====== ANOVA (Mixed Design) ======
#> 
#> Descriptives:
#> ─────────────────────────────
#>  "A" "C" "B"   Mean    S.D. n
#> ─────────────────────────────
#>   A1  C1  B1  4.000 (1.414) 4
#>   A1  C1  B2  4.000 (1.633) 4
#>   A1  C2  B1  4.750 (2.062) 4
#>   A1  C2  B2  3.750 (0.957) 4
#>   A2  C1  B1  8.000 (0.816) 4
#>   A2  C1  B2  8.000 (0.816) 4
#>   A2  C2  B1  6.000 (0.816) 4
#>   A2  C2  B2 12.000 (0.816) 4
#> ─────────────────────────────
#> Total sample size: N = 16
#> 
#> ANOVA Table:
#> Dependent variable(s):      B1, B2
#> Between-subjects factor(s): A, C
#> Within-subjects factor(s):  B
#> Covariate(s):               –
#> ──────────────────────────────────────────────────────────────────────────
#>                 MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ──────────────────────────────────────────────────────────────────────────
#> A          153.125 2.542   1  12 60.246 <.001 ***   .834 [.639, .906] .803
#> C            3.125 2.542   1  12  1.230  .289       .093 [.000, .390] .077
#> A * C        1.125 2.542   1  12  0.443  .518       .036 [.000, .305] .029
#> B           12.500 0.583   1  12 21.429 <.001 ***   .641 [.308, .795] .250
#> A * B       24.500 0.583   1  12 42.000 <.001 ***   .778 [.532, .874] .395
#> C * B       12.500 0.583   1  12 21.429 <.001 ***   .641 [.308, .795] .250
#> A * C * B   24.500 0.583   1  12 42.000 <.001 ***   .778 [.532, .874] .395
#> ──────────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ────────────────────────────────────
#>         Levene’s F df1 df2     p    
#> ────────────────────────────────────
#> DV: B1       0.946   3  12  .449    
#> DV: B2       0.423   3  12  .740    
#> ────────────────────────────────────
#> 
#> Mauchly’s Test of Sphericity:
#> The repeated measures have only two levels. The assumption of sphericity is always met.
#> 


#### Other Examples ####

data.new = mixed.3_1b2w
names(data.new) = c("Group", "Cond_01", "Cond_02", "Cond_03", "Cond_04")
MANOVA(data.new,
       dvs="Cond_01:Cond_04",
       dvs.pattern="Cond_(..)",
       between="Group",
       within="Condition")  # rename the factor
#> 
#> Note:
#> dvs="Cond_01:Cond_04" is matched to variables:
#> Cond_01, Cond_02, Cond_03, Cond_04
#> 
#> ====== ANOVA (Mixed Design) ======
#> 
#> Descriptives:
#> ─────────────────────────────────────
#>  "Group" "Condition"   Mean    S.D. n
#> ─────────────────────────────────────
#>   Group1 Condition01  4.000 (1.414) 4
#>   Group1 Condition02  4.750 (2.062) 4
#>   Group1 Condition03  4.000 (1.633) 4
#>   Group1 Condition04  3.750 (0.957) 4
#>   Group2 Condition01  8.000 (0.816) 4
#>   Group2 Condition02  6.000 (0.816) 4
#>   Group2 Condition03  8.000 (0.816) 4
#>   Group2 Condition04 12.000 (0.816) 4
#> ─────────────────────────────────────
#> Total sample size: N = 8
#> 
#> ANOVA Table:
#> Dependent variable(s):      Cond_01, Cond_02, Cond_03, Cond_04
#> Between-subjects factor(s): Group
#> Within-subjects factor(s):  Condition
#> Covariate(s):               –
#> ──────────────────────────────────────────────────────────────────────────────────
#>                         MS   MSE df1 df2      F     p     η²p [90% CI of η²p]  η²G
#> ──────────────────────────────────────────────────────────────────────────────────
#> Group              153.125 4.708   1   6 32.522  .001 **    .844 [.503, .926] .803
#> Condition            9.375 0.514   3  18 18.243 <.001 ***   .753 [.533, .843] .429
#> Group * Condition   16.708 0.514   3  18 32.514 <.001 ***   .844 [.702, .902] .572
#> ──────────────────────────────────────────────────────────────────────────────────
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ─────────────────────────────────────────
#>              Levene’s F df1 df2     p    
#> ─────────────────────────────────────────
#> DV: Cond_01       1.000   1   6  .356    
#> DV: Cond_02       1.485   1   6  .269    
#> DV: Cond_03       0.600   1   6  .468    
#> DV: Cond_04       0.500   1   6  .506    
#> ─────────────────────────────────────────
#> 
#> Mauchly’s Test of Sphericity:
#> ────────────────────────────────────────
#>                    Mauchly's W     p    
#> ────────────────────────────────────────
#> Condition               0.5544  .738    
#> Group * Condition       0.5544  .738    
#> ────────────────────────────────────────
#> 

# ?afex::obk.long
MANOVA(afex::obk.long,
       subID="id",
       dv="value",
       between=c("treatment", "gender"),
       within=c("phase", "hour"),
       cov="age",
       sph.correction="GG")
#> 
#>     * Data are aggregated to mean (across items/trials)
#>     if there are >=2 observations per subject and cell.
#>     You may use Linear Mixed Model to analyze the data,
#>     e.g., with subjects and items as level-2 clusters.
#> 
#> ====== ANOVA (Mixed Design) ======
#> 
#> Descriptives:
#> ─────────────────────────────────────────────────────
#>  "treatment" "gender" "phase" "hour"   Mean    S.D. n
#> ─────────────────────────────────────────────────────
#>      control        F    fup   hour1  4.000 (0.000) 2
#>      control        F    fup   hour2  3.500 (0.707) 2
#>      control        F    fup   hour3  5.500 (0.707) 2
#>      control        F    fup   hour4  3.500 (0.707) 2
#>      control        F    fup   hour5  3.500 (0.707) 2
#>      control        F    post  hour1  4.000 (2.828) 2
#>      control        F    post  hour2  4.500 (3.536) 2
#>      control        F    post  hour3  5.500 (3.536) 2
#>      control        F    post  hour4  5.500 (0.707) 2
#>      control        F    post  hour5  3.000 (0.000) 2
#>      control        F    pre   hour1  4.000 (1.414) 2
#>      control        F    pre   hour2  4.000 (0.000) 2
#>      control        F    pre   hour3  6.500 (0.707) 2
#>      control        F    pre   hour4  4.500 (0.707) 2
#>      control        F    pre   hour5  3.500 (0.707) 2
#>      control        M    fup   hour1  4.333 (2.517) 3
#>      control        M    fup   hour2  4.667 (1.528) 3
#>      control        M    fup   hour3  5.667 (3.512) 3
#>      control        M    fup   hour4  5.000 (1.732) 3
#>      control        M    fup   hour5  3.667 (2.517) 3
#>      control        M    post  hour1  3.000 (1.000) 3
#>      control        M    post  hour2  3.000 (1.732) 3
#>      control        M    post  hour3  5.000 (2.000) 3
#>      control        M    post  hour4  4.333 (1.155) 3
#>      control        M    post  hour5  3.000 (1.000) 3
#>      control        M    pre   hour1  3.333 (2.082) 3
#>      control        M    pre   hour2  4.000 (2.000) 3
#>      control        M    pre   hour3  4.667 (0.577) 3
#>      control        M    pre   hour4  4.000 (2.646) 3
#>      control        M    pre   hour5  4.000 (3.000) 3
#>      A              F    fup   hour1  5.500 (0.707) 2
#>      A              F    fup   hour2  5.000 (1.414) 2
#>      A              F    fup   hour3  7.000 (0.000) 2
#>      A              F    fup   hour4  5.000 (0.000) 2
#>      A              F    fup   hour5  5.000 (1.414) 2
#>      A              F    post  hour1  3.000 (1.414) 2
#>      A              F    post  hour2  4.500 (0.707) 2
#>      A              F    post  hour3  7.000 (1.414) 2
#>      A              F    post  hour4  5.000 (1.414) 2
#>      A              F    post  hour5  3.000 (2.828) 2
#>      A              F    pre   hour1  2.500 (0.707) 2
#>      A              F    pre   hour2  3.000 (0.000) 2
#>      A              F    pre   hour3  4.500 (0.707) 2
#>      A              F    pre   hour4  4.500 (2.121) 2
#>      A              F    pre   hour5  3.000 (1.414) 2
#>      A              M    fup   hour1  8.500 (0.707) 2
#>      A              M    fup   hour2  9.500 (0.707) 2
#>      A              M    fup   hour3 11.000 (0.000) 2
#>      A              M    fup   hour4  9.000 (0.000) 2
#>      A              M    fup   hour5  7.000 (1.414) 2
#>      A              M    post  hour1  8.000 (1.414) 2
#>      A              M    post  hour2  8.000 (1.414) 2
#>      A              M    post  hour3  9.000 (1.414) 2
#>      A              M    post  hour4  9.000 (1.414) 2
#>      A              M    post  hour5  8.500 (0.707) 2
#>      A              M    pre   hour1  6.000 (1.414) 2
#>      A              M    pre   hour2  6.500 (2.121) 2
#>      A              M    pre   hour3  6.500 (0.707) 2
#>      A              M    pre   hour4  6.500 (3.536) 2
#>      A              M    pre   hour5  7.000 (2.828) 2
#>      B              F    fup   hour1  6.750 (0.500) 4
#>      B              F    fup   hour2  7.250 (0.500) 4
#>      B              F    fup   hour3  8.500 (1.000) 4
#>      B              F    fup   hour4  7.500 (1.915) 4
#>      B              F    fup   hour5  6.250 (2.217) 4
#>      B              F    post  hour1  5.500 (1.291) 4
#>      B              F    post  hour2  6.250 (0.500) 4
#>      B              F    post  hour3  7.000 (0.816) 4
#>      B              F    post  hour4  7.000 (1.826) 4
#>      B              F    post  hour5  5.500 (2.380) 4
#>      B              F    pre   hour1  3.250 (1.500) 4
#>      B              F    pre   hour2  3.500 (1.732) 4
#>      B              F    pre   hour3  4.750 (2.062) 4
#>      B              F    pre   hour4  4.500 (2.887) 4
#>      B              F    pre   hour5  4.000 (1.633) 4
#>      B              M    fup   hour1  7.000 (1.732) 3
#>      B              M    fup   hour2  7.000 (1.000) 3
#>      B              M    fup   hour3  9.000 (1.000) 3
#>      B              M    fup   hour4  7.000 (1.000) 3
#>      B              M    fup   hour5  6.667 (1.528) 3
#>      B              M    post  hour1  6.667 (2.082) 3
#>      B              M    post  hour2  7.000 (3.000) 3
#>      B              M    post  hour3  8.000 (2.646) 3
#>      B              M    post  hour4  7.333 (2.082) 3
#>      B              M    post  hour5  6.000 (2.000) 3
#>      B              M    pre   hour1  4.333 (1.528) 3
#>      B              M    pre   hour2  4.667 (2.082) 3
#>      B              M    pre   hour3  5.667 (2.082) 3
#>      B              M    pre   hour4  3.667 (2.082) 3
#>      B              M    pre   hour5  3.333 (0.577) 3
#> ─────────────────────────────────────────────────────
#> Total sample size: N = 16
#> 
#> ANOVA Table:
#> Dependent variable(s):      value
#> Between-subjects factor(s): treatment, gender
#> Within-subjects factor(s):  phase, hour
#> Covariate(s):               age
#> ───────────────────────────────────────────────────────────────────────────────────────────────────────
#>                                        MS    MSE   df1    df2      F     p     η²p [90% CI of η²p]  η²G
#> ───────────────────────────────────────────────────────────────────────────────────────────────────────
#> treatment                          85.700 23.962 2.000  9.000  3.577  .072 .     .443 [.000, .684] .294
#> gender                             94.598 23.962 1.000  9.000  3.948  .078 .     .305 [.000, .610] .187
#> age                                12.399 23.962 1.000  9.000  0.517  .490       .054 [.000, .381] .029
#> treatment * gender                 30.766 23.962 2.000  9.000  1.284  .323       .222 [.000, .516] .130
#> phase                              79.287  3.909 1.697 15.277 20.281 <.001 ***   .693 [.420, .813] .246
#> treatment * phase                  23.743  3.909 3.395 15.277  6.073  .005 **    .574 [.192, .728] .164
#> gender * phase                      0.963  3.909 1.697 15.277  0.246  .749       .027 [.000, .193] .004
#> age * phase                        12.108  3.909 1.697 15.277  3.097  .081 .     .256 [.000, .502] .048
#> treatment * gender * phase          6.261  3.909 3.395 15.277  1.601  .228       .262 [.000, .470] .049
#> hour                               50.786  2.475 2.137 19.230 20.519 <.001 ***   .695 [.459, .804] .209
#> treatment * hour                    1.766  2.475 4.273 19.230  0.714  .601       .137 [.000, .271] .018
#> gender * hour                       1.753  2.475 2.137 19.230  0.708  .514       .073 [.000, .254] .009
#> age * hour                          6.976  2.475 2.137 19.230  2.818  .082 .     .238 [.000, .456] .035
#> treatment * gender * hour           1.459  2.475 4.273 19.230  0.590  .684       .116 [.000, .233] .015
#> phase * hour                        2.802  2.826 3.485 31.362  0.991  .419       .099 [.000, .223] .023
#> treatment * phase * hour            0.944  2.826 6.969 31.362  0.334  .932       .069 [.000, .027] .016
#> gender * phase * hour               2.540  2.826 3.485 31.362  0.899  .465       .091 [.000, .210] .021
#> age * phase * hour                  2.164  2.826 3.485 31.362  0.766  .540       .078 [.000, .188] .018
#> treatment * gender * phase * hour   1.840  2.826 6.969 31.362  0.651  .710       .126 [.000, .170] .030
#> ───────────────────────────────────────────────────────────────────────────────────────────────────────
#> Sphericity correction method: GG (Greenhouse-Geisser)
#> MSE = mean square error (the residual variance of the linear model)
#> η²p = partial eta-squared = SS / (SS + SSE) = F * df1 / (F * df1 + df2)
#> ω²p = partial omega-squared = (F - 1) * df1 / (F * df1 + df2 + 1)
#> η²G = generalized eta-squared (see Olejnik & Algina, 2003)
#> Cohen’s f² = η²p / (1 - η²p)
#> 
#> Levene’s Test for Homogeneity of Variance:
#> ────────────────────────────────────────────
#>                 Levene’s F df1 df2     p    
#> ────────────────────────────────────────────
#> DV: pre_hour1        1.019   5  10  .456    
#> DV: pre_hour2        3.233   5  10  .054 .  
#> DV: pre_hour3        5.654   5  10  .010 ** 
#> DV: pre_hour4        0.793   5  10  .578    
#> DV: pre_hour5        1.208   5  10  .372    
#> DV: post_hour1       1.831   5  10  .194    
#> DV: post_hour2       2.664   5  10  .088 .  
#> DV: post_hour3       2.566   5  10  .096 .  
#> DV: post_hour4       1.570   5  10  .254    
#> DV: post_hour5       1.773   5  10  .206    
#> DV: fup_hour1        3.012   5  10  .065 .  
#> DV: fup_hour2        1.392   5  10  .306    
#> DV: fup_hour3        2.672   5  10  .087 .  
#> DV: fup_hour4        3.362   5  10  .049 *  
#> DV: fup_hour5        0.679   5  10  .650    
#> ────────────────────────────────────────────
#> 
#> Mauchly’s Test of Sphericity:
#> ────────────────────────────────────────────────────────
#>                                    Mauchly's W     p    
#> ────────────────────────────────────────────────────────
#> phase                                   0.8218  .456    
#> treatment * phase                       0.8218  .456    
#> gender * phase                          0.8218  .456    
#> age * phase                             0.8218  .456    
#> treatment * gender * phase              0.8218  .456    
#> hour                                    0.0967  .049 *  
#> treatment * hour                        0.0967  .049 *  
#> gender * hour                           0.0967  .049 *  
#> age * hour                              0.0967  .049 *  
#> treatment * gender * hour               0.0967  .049 *  
#> phase * hour                            0.0002  .087 .  
#> treatment * phase * hour                0.0002  .087 .  
#> gender * phase * hour                   0.0002  .087 .  
#> age * phase * hour                      0.0002  .087 .  
#> treatment * gender * phase * hour       0.0002  .087 .  
#> ────────────────────────────────────────────────────────
#> 
# }