Reliability analysis and PCA of a dictionary.

Reliability analysis (Cronbach's \(\alpha\) and average cosine similarity) and Principal Component Analysis (PCA) of a dictionary, with visualization of cosine similarities between words (ordered by the first principal component loading). Note that Cronbach's \(\alpha\) can be misleading when the number of items/words is large.

Usage

dict_reliability(
  data,
  words = NULL,
  pattern = NULL,
  alpha = TRUE,
  sort = TRUE,
  plot = TRUE,
  ...
)

Arguments

data

A wordvec (data.table) or embed (matrix), see data_wordvec_load.

words

[Option 1] Character string(s).

pattern

[Option 2] Regular expression (see str_subset). If neither words nor pattern are specified (i.e., both are NULL), then all words in the data will be extracted.

alpha

Estimate the Cronbach's \(\alpha\)? Defaults to TRUE. Note that this can be misleading and time-consuming when the number of items/words is large.

sort

Sort items by the first principal component loading (PC1)? Defaults to TRUE.

plot

Visualize the cosine similarities? Defaults to TRUE.

...

Other parameters passed to plot_similarity.

Value

A list object of new class reliability:

alpha

Cronbach's \(\alpha\)

eigen

Eigen values from PCA

pca

PCA (only 1 principal component)

pca.rotation

PCA with varimax rotation (if potential principal components > 1)

items

Item statistics

cos.sim.mat

A matrix of cosine similarities of all word pairs

cos.sim

Lower triangular part of the matrix of cosine similarities

Download

Download pre-trained word vectors data (.RData): https://psychbruce.github.io/WordVector_RData.pdf

References

Nicolas, G., Bai, X., & Fiske, S. T. (2021). Comprehensive stereotype content dictionaries using a semi-automated method. European Journal of Social Psychology, 51(1), 178--196.

See also

cosine_similarity

pair_similarity

plot_similarity

tab_similarity

most_similar

dict_expand

Examples

d = as_embed(demodata, normalize=TRUE)

dict = dict_expand(d, "king")
#> ── Iteration 1 (threshold of cosine similarity = 0.5) ──────────────────────────
#> ✔ 3 more words appended: "queen", "royal", and "King"
#> 
#> ── Iteration 2 (threshold of cosine similarity = 0.5) ──────────────────────────
#> ✔ 2 more words appended: "Queen" and "Prince"
#> 
#> ── Iteration 3 (threshold of cosine similarity = 0.5) ──────────────────────────
#> ✔ No more word appended. Successfully convergent.
#> 
#> ── Finish (convergent) ──
#> 
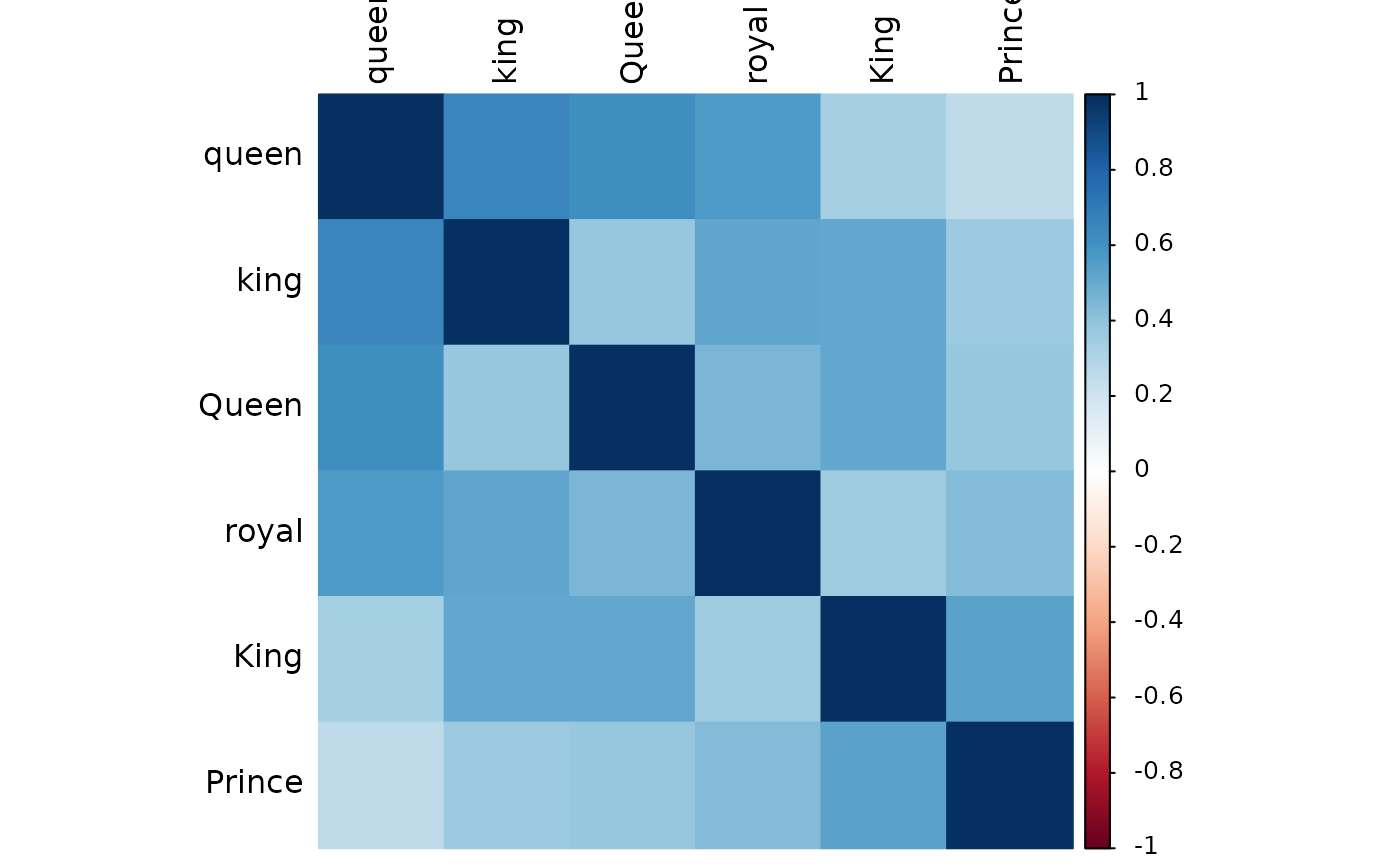
dict_reliability(d, dict)
#> ! Results may be inaccurate if word vectors are not normalized.
#> ✔ All word vectors now have been automatically normalized.

#> 
#> ── Reliability Analysis and PCA of Dictionary ──────────────────────────────────
#> 
#> Number of items = 6
#> Mean cosine similarity = 0.459
#> Cronbach’s α = 0.836 (misleading when N of items is large)
#> Variance explained by PC1 = 55.2%
#> Potential principal components = 1 (with eigen value > 1)
#> 
#> Cosine Similarities Between Words:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>  0.2584  0.3715  0.4588  0.4590  0.5273  0.6511 
#> 
#> Item Statistics:
#> ────────────────────────────────────────────────────
#>         PC1 Loading Item-SumVec Sim. Item-Rest Corr.
#> ────────────────────────────────────────────────────
#> queen         0.785            0.769           0.650
#> king          0.781            0.772           0.653
#> Queen         0.760            0.755           0.631
#> royal         0.754            0.751           0.624
#> King          0.723            0.732           0.597
#> Prince        0.645            0.668           0.511
#> ────────────────────────────────────────────────────
#> PC1 Loading = the first principal component loading
#> Item-SumVec Sim. = cosine similarity with the sum vector
#> Item-Rest Corr. = corrected item-total correlation

dict.cn = dict_expand(d, "China", threshold=0.65)
#> 
#> ── Iteration 1 (threshold of cosine similarity = 0.65) ─────────────────────────
#> ✔ 4 more words appended: "Chinese", "Beijing", "Taiwan", and "Shanghai"
#> 
#> ── Iteration 2 (threshold of cosine similarity = 0.65) ─────────────────────────
#> ✔ 4 more words appended: "Guangzhou", "Taiwanese", "Shenzhen", and "Li"
#> 
#> ── Iteration 3 (threshold of cosine similarity = 0.65) ─────────────────────────
#> ✔ 3 more words appended: "Wang", "Chen", and "yuan"
#> 
#> ── Iteration 4 (threshold of cosine similarity = 0.65) ─────────────────────────
#> ✔ No more word appended. Successfully convergent.
#> 
#> ── Finish (convergent) ──
#> 
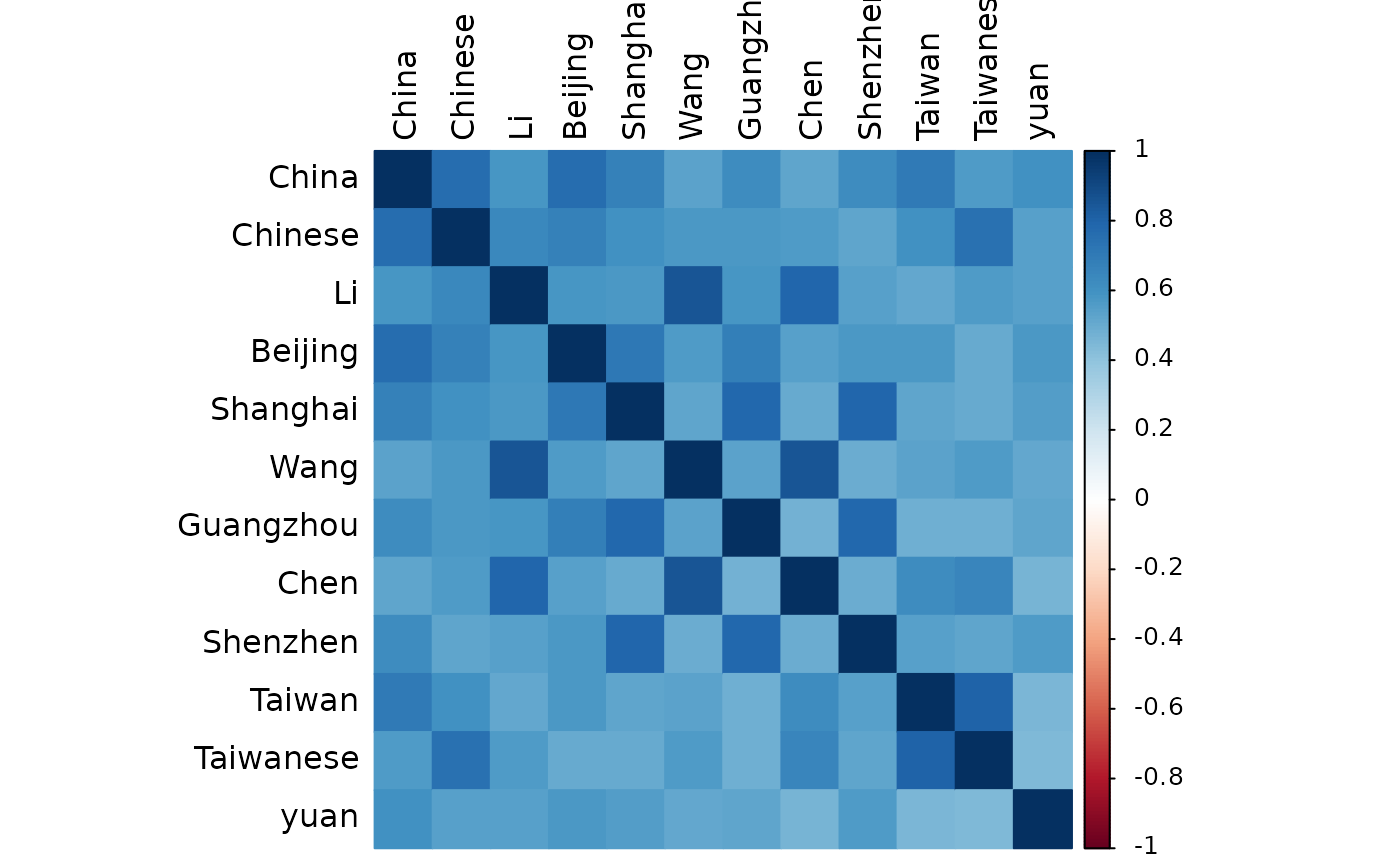
dict_reliability(d, dict.cn)
#> ! Results may be inaccurate if word vectors are not normalized.
#> ✔ All word vectors now have been automatically normalized.

#> 
#> ── Reliability Analysis and PCA of Dictionary ──────────────────────────────────
#> 
#> Number of items = 12
#> Mean cosine similarity = 0.596
#> Cronbach’s α = 0.946 (misleading when N of items is large)
#> Variance explained by PC1 = 63.0%
#> Potential principal components = 2 (with eigen value > 1)
#> 
#> Cosine Similarities Between Words:
#>    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
#>  0.4474  0.5266  0.5666  0.5963  0.6395  0.8555 
#> 
#> Item Statistics:
#> ───────────────────────────────────────────────────────
#>            PC1 Loading Item-SumVec Sim. Item-Rest Corr.
#> ───────────────────────────────────────────────────────
#> China            0.839            0.837           0.801
#> Chinese          0.823            0.822           0.781
#> Beijing          0.822            0.817           0.780
#> Li               0.818            0.819           0.778
#> Shanghai         0.817            0.815           0.775
#> Wang             0.793            0.793           0.749
#> Guangzhou        0.791            0.792           0.745
#> Chen             0.786            0.787           0.741
#> Shenzhen         0.781            0.783           0.735
#> Taiwan           0.773            0.775           0.726
#> Taiwanese        0.770            0.773           0.723
#> yuan             0.704            0.711           0.651
#> ───────────────────────────────────────────────────────
#> PC1 Loading = the first principal component loading
#> Item-SumVec Sim. = cosine similarity with the sum vector
#> Item-Rest Corr. = corrected item-total correlation

dict_reliability(d, c(dict, dict.cn))
#> ! Results may be inaccurate if word vectors are not normalized.
#> ✔ All word vectors now have been automatically normalized.

#> 
#> ── Reliability Analysis and PCA of Dictionary ──────────────────────────────────
#> 
#> Number of items = 18
#> Mean cosine similarity = 0.331
#> Cronbach’s α = 0.899 (misleading when N of items is large)
#> Variance explained by PC1 = 42.4%
#> Potential principal components = 4 (with eigen value > 1)
#> 
#> Cosine Similarities Between Words:
#>     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
#> -0.06071  0.07339  0.38084  0.33065  0.56430  0.85546 
#> 
#> Item Statistics:
#> ───────────────────────────────────────────────────────
#>            PC1 Loading Item-SumVec Sim. Item-Rest Corr.
#> ───────────────────────────────────────────────────────
#> China            0.832            0.741           0.695
#> Chinese          0.821            0.751           0.705
#> Li               0.819            0.763           0.719
#> Beijing          0.818            0.743           0.699
#> Shanghai         0.812            0.741           0.695
#> Wang             0.794            0.742           0.695
#> Chen             0.789            0.747           0.702
#> Guangzhou        0.786            0.714           0.663
#> Taiwan           0.774            0.723           0.673
#> Taiwanese        0.772            0.726           0.676
#> Shenzhen         0.772            0.685           0.630
#> yuan             0.697            0.631           0.569
#> royal            0.178            0.406           0.329
#> Queen            0.154            0.392           0.308
#> king             0.141            0.382           0.302
#> King             0.127            0.361           0.277
#> queen            0.124            0.364           0.286
#> Prince           0.085            0.305           0.218
#> ───────────────────────────────────────────────────────
#> PC1 Loading = the first principal component loading
#> Item-SumVec Sim. = cosine similarity with the sum vector
#> Item-Rest Corr. = corrected item-total correlation
# low-loading items should be removed